1 개요
우리가 여러 개의 문자열을 가지고 있을 때, 어떤 문자열이 그 문자열 중 하나인지 알아내는 방법은 뭐가 있을까?
단순하게 일일이 비교해보면 된다. 하지만 컴퓨터는 이러한 방법이 매우 비효율적이다. 예를 들어, 최대 길이가 [math]m[/math]인 문자열 [math]n[/math]개의 집합에서 마찬가지로 최대 길이가 [math]m[/math]인 임의의 문자열이 그 문자열들의 집합에 포함되는지를 일일이 확인하면 사전처리는 필요 없지만, 최악의 경우 [math]O(nm)[/math]의 비교 횟수가 필요하다.
이 문자열을 정렬시킨 뒤, 이진 탐색이라는 강력한 알고리즘을 사용하면 [math]O(m \log n)[/math]로 단축시킬 수 있지만, 정렬 과정 자체에 [math]O(n m \log n)[/math][1]의 시간이 걸리므로 사양이 안 좋은 컴퓨터라면 이것도 비효율적이다. 하지만 위의 시간 복잡도를 압도하는 알고리즘이 존재한다. 프레드킨이 이름 붙인 "Trie"[2]라는 자료구조가 지금부터 설명할 가장 효율적인 문자열 검색법이다.
2 구조
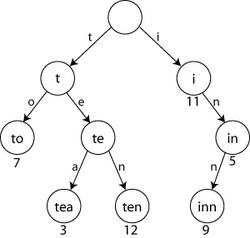
기본적으로 K진 트리[3]의 구조를 띠고 있다. 영어사전을 생각해보면 간단하다. 우리가 'cancel'이라는 단어를 찾으려면 우선 앞 글자 'c'의 색인을 찾을 것이다. 그 다음 'a', 'n', ... 순서대로 찾아가는 것이다. 이것을 논리적으로 컴퓨터에 적용한 구조가 바로 트라이 구조이다.[4] 이를테면 'tea'라는 문자열이 입력되었다면 순서대로 머릿글자 't'가 등록되고 그 다음 'e'가, 그 다음 'a'가 등록된다. 마지막에 문자열을 모두 찾았다면 그 위치에 "이곳에 문자열이 있소!" 하고 표시하면 되는 것이다. 그리고 그런 시작 문자열을 접두어(prefix)라고 부른다.
이러한 트라이 구조는 찾고자 하는 문자열을 공간을 많이 사용하는 대신, 그 문자열의 길이의 속도만큼 초고속 탐색이 가능하다.
일반적으로는 동적 할당을 통해 생성하지만 Array를 통하여 구축하는 방법을 설명한다.
우선 트라이에 등록하고자 하는 문자열 p 가 있다고 하자. (편의상 이 문자열은 알파벳 소문자로만 구성되어 있다고 가정하자.)
그리고 trie의 루트는 언제나 0이다. 그리고 이 0 부터 시작하여 p[i]-'a' 에 대해 다음 노드로 이동 가능한지 여부를 판단한다.
이동 할 수 있다면 이동하고 이동 할 수 없다면 triesize에 1을 추가하여 새로운 노드를 만든 뒤 그곳을 가르키게 한다.
동적 할당을 활용할 수 있는 전문가라면, 할당 해준 뒤, 그 것을 가르키게 하면 된다.
이하 반복.
triesize는 코드 시작부에서 0으로 초기화 한다.
node = 0 for i in 0..p.length if trie[node][p[i]-'a'] == 0 trie[node][p[i]-'a'] = ++triesize node = triesize else node = trie[node][p[i]='a']; check[node] = true; // 해당 노드에 문자열이 존재함을 알림
2.1 시간 복잡도
문자열 집합의 개수와 상관 없이 찾고자 하는 문자열의 길이가 시간 복잡도가 된다. 즉, 문자열의 길이가 [math]m[/math]이라면 시간 복잡도는 [math]O(m)[/math]. 그 이유는 간단하다. 트라이를 구현할 때, [math]n[/math]과 [math]m[/math]이 상대적으로 작다면[6] 배열을 사용할 텐데, 현재 노드의 위치를 i, j번째 문자라고 한다면 trie[i][j]의 위치를 조회하는 건 [math]O(1)[/math]에 수행이 가능하다. 여기서 [math]m[/math]번을 수행하니 [math]O(m)[/math]의 시간이 걸리는 것이다. 하지만 [math]n[/math]과 [math]m[/math]이 큰 경우에는, 메모리 확보를 위해 시간을 희생해서라도 n이 진짜 무식하게 큰 게 아닌 이상 의미없다. Map이나 이진 트리 등으로 트라이를 만들기도 한다. 이 경우엔 [math]O(m \log n)[/math]의 시간이 소모된다.
3 관련 알고리즘
- ↑ 이것은 사전처리이므로 한 번만 수행하면 된다. 후술할 트라이의 경우는 사전처리를 [math]O(nm)[/math] 안에 할 수 있다. 단, Map이나 이진 트리를 사용하는 경우 제외.
- ↑ 발음은 트리(tree)가 아니다. 트라이(try)다.
- ↑ 여기서의 K는 문자의 개수를 의미한다. 예를 들어 63개의 문자를 사용한다면 63진 트리가 되는 것이다.
- ↑ The Art Of Computer Programming 3 561P 숫자별 검색
- ↑ 사진 출처
- ↑ 여기서 [math]n[/math]과 [math]m[/math]이 작다는 것은 노드의 개수로 인한 메모리 사용량이 일반 가정집에서 안정적으로 확보할 수 있는 256MB를 넘지 않는 걸로 한다.
- ↑ 오늘날 검색엔진의 주가 되는 알고리즘이다.