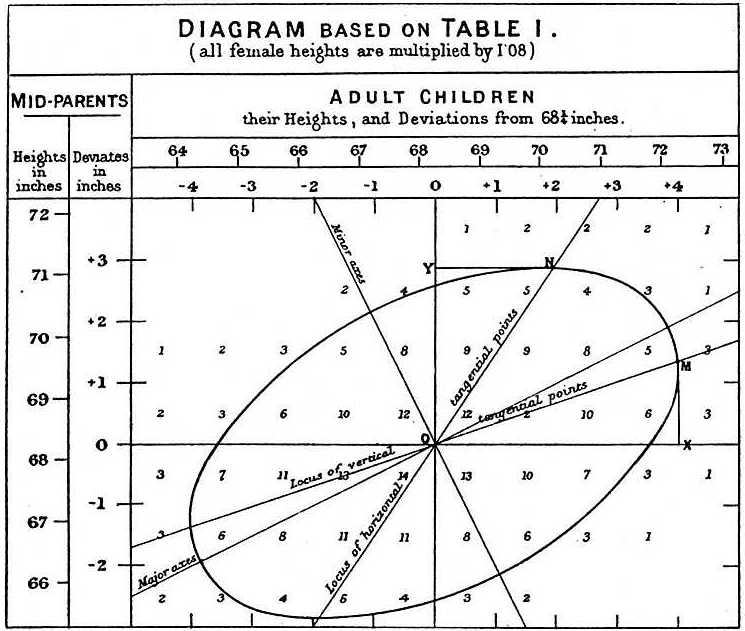
Regression towards mediocrity (평균으로의 회귀) 현상을 궁금하게 여겼던 생물학자 프랜시스 갈튼은 부모와 그 자식의 키에 대한 자료를 만들어 205명의 부모와 그들의 자식 930명의 키에 대한 자료를 분석하여 회귀계수가 2/3임을 밝혔다. (가우스의 최소제곱법을 쓰지 않고 타원으로 적합시켜 회귀계수가 2/3임을 찾아낸 것이 특이하다.) 즉, 키는 유전적인 요소가 강력하게 작용한다는 것을 밝힌 것이다. 갈튼은 산점도에 최초로 선형식을 표현하여 오늘날의 회귀분석을 성립하는데 지대한 공을 세웠다.
외계어 같지만 사실 회귀모형은 'x 와 y 의 관계' 를 한단어로 적어놓은것 뿐이다.
좀더 정확히는 여러개의 변수(x,y,z 등) 사이에 서로 이루고 있는 관계를 어떤 형태로 표현(보통 수학 공식이 된다)하고, 그렇게 만들어진 형태를 '모형' 이라 칭하면서 회귀'모형' 이 되는것.
그럼 그냥 '모형' 이라고 부르면 되는데 굳이 회귀모형 이라고 '회귀'한단어를 덧붙인 이유는, 일반적으로 수학은 원인(x)이 주어지면 결과(y)를 계산하는 형태로 가지만, 경제학에서는 결과(y)에서 원인(x)을 역산해야 할 일이 훨씬 많기 때문이다.
즉.
일반적으로 가는 방향(원인에서 결과 x->y)이 아니고 거꾸로(x<-y) 가기 때문에 되돌아 간다 라는 의미에서 회귀 라는 표현을 더한것이다.[1]
사실 이것도 파고들면 '공식' 대신 '모형'이라는 표현을 쓴 이유가 있는데, 일반적인 과학은 반복실험으로 검증이 가능한 반면 경제학은 반복실험을 통한 검증이 불가능하다.[2] 그러다보니 경제학에서는 대부분의 경우 결과에서 원인을 역산해 놔도 검증이 불가능 하다 보니 '아마도 이럴 것이다' 라는 가설 형태에서 더이상 나아가질 못하는 경우가 많은데, 거기서 멈춘게 바로 '모형' 이 된다.
달리 말하면.
어떤 경제현상의 결과를 보고, 아마도 이런 원인 때문일 것이다. 라고 이론을 세워 놓으면, 그게 회귀모형이 된다.