1 개요
논리학과 수학의 법칙 중 하나로, 논리합은 논리곱과 부정기호로, 논리곱은 논리합과 부정기호로 표현할 수 있음을 가리키는 법칙이다.
일반적인 표현으로
[math]\text{not}(A \text{ or } B) = (\text{not} A) \text{ and } (\text{not} B)[/math]
[math]\text{not} (A \text{ and } B) = (\text{not} A) \text{ or } (\text{not} B)[/math]
논리곱(합)의 부정은 각각 부정의 논리합(곱)과 같다는 법칙. 이는 논리학과 동일하게 집합론, 전자회로등에서도 똑같이 사용된다.
아래는 동일한 내용을 각각의 학문에서 주로 사용하는 수식으로 표현한 것이다.
논리학[math]\neg (p \lor q) = \neg p \land \neg q[/math]
[math]\neg (p \land q) = \neg p \lor \neg q[/math]
집합론[math](A\cup B)^c = A^c \cap B^c [/math]
[math](A\cap B)^c = A^c \cup B^c [/math]
전자회로[math]\overline{(A + B)} = \overline{A} \cdot \overline{B}[/math]
[math]\overline{(A \cdot B)} = \overline{A} + \overline{B}[/math]
수학자 어거스트 드 모르간에 의해 증명되었으며, 이 수학자의 이름이 붙어 있다.
2 벤다이어그램으로 본 법칙
제일 먼저 이를 접하게 되는 것은 집합에서 '벤다이어그램'으로 이 둘이 같다는 것을 보여주는 형태로 나타난다.

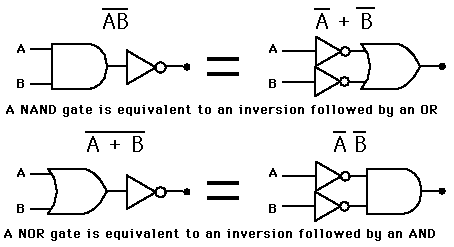
3 전자회로에서의 응용
전자회로 등에서는 약간 응용해서 [math]A + B = \overline{ \overline{A} \cdot \overline{B}}[/math] 나 [math]A \cdot B = \overline{\overline{A} + \overline{B}}[/math] 형식으로 표현하는 경우도 있지만, 위의 같은 식이란 것을 쉽게 유도할 수 있다.
- ↑ 참고로 이것만으로 만든 메모리가 바로 우리가 일반적으로 부르는 낸드플래시 메모리(NAND flach memory)이다. NAND게이트 만으로 만든 녀석이라 낸드플래시라고하며, 비슷한 원리로 NOR만으로 만든 녀석도 있는데, 이쪽은 노어(NOR)플래시라고 부른다. 다만 낸드에 비해 가성비가 안나와서 현재는 하향추세