1 개요
강체의 회전운동에서 회전축이 외부 돌림힘으로 인해 비틀어지는 운동. 각운동량의 변화에 따라 회전축이 돌아간다.
이 돌림힘은 회전하는 강체를 '쓰러뜨리는' 경우와 '똑바로 세우는' 경우로 나누어서 생각해볼 수 있다.
보다 자세한 운동의 기술은 장동운동 참고.
2 자이로스코프와 팽이의 세차운동
이미지 출처
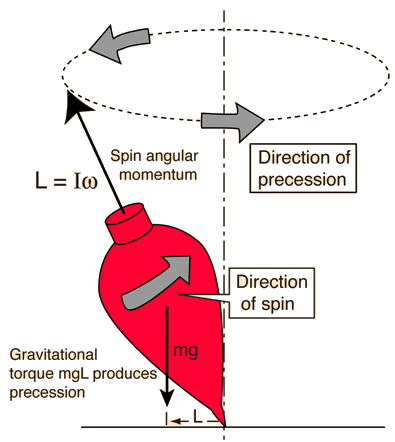
회전하지 않는 상태로는 팽이나 자이로스코프는 아래로 떨어진다. 하지만 각운동량이 있다면 상황은 달라진다.
위 그림과 같이 바닥 위에서 팽이가 돌 때 쓰러지는 방향으로 돌림힘을 받고 있다. 만약 바로 아래로 쓰러진다고 하면 각운동량 벡터도 따라서 기울어져야 하는데, 그렇게 운동하려면 그에 상응하는 돌림힘이 존재해야 한다. 그러나 정작 팽이를 쓰러뜨리려는 중력은 돌림힘의 방향을 위 그림 기준으로 나오는 방향으로 작용한다. 결국 각운동량 벡터는 아래로 쓰러지는 대신 옆으로 뒤틀리고, 그에 따라 팽이도 방향을 틀게 된다.
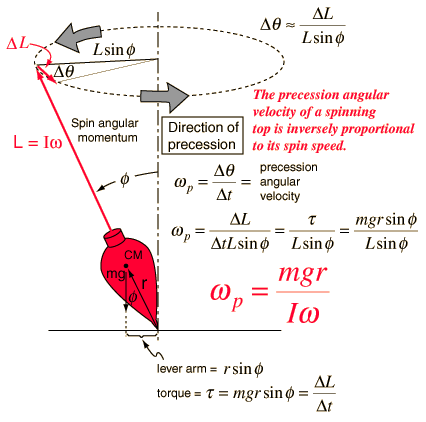
다음과 같이 식이 세워진다.
[math] \dot{\vec{L}}= \vec{\tau} = \vec{r}\times m\vec{g} = mgr \hat{k} \times \hat{r} [/math]
[math] \dot{\vec{L}}= \vec{\omega_{p}} \times \vec{L} = \omega_{p}\cdot I\omega \hat{k} \times \hat{r} [/math]
위아래를 견주면 세차운동의 각속도를 알 수 있다.
[math] \omega_{p}= \frac{mgr}{I\omega}, \omega_{p}= \frac{mgr}{I\omega}\hat{k} [/math]
여기서 [math]\hat{k}, \hat{r}[/math]은 각각 수직한 방향과 팽이의 방향을 나타내는 단위벡터이다.
이 상황에서 팽이의 회전 방향과 세차운동 방향은 같다. 엄밀히는 두 벡터 [math] \vec{\omega_{p}}, \vec{L}[/math]이 이루는 각은 예각이다.
3 지구의 세차운동

이미지 출처
세차운동으로 인한 천구의 북극과 북극성의 변화

이미지 출처
지구의 세차운동
지구는 자전을 하므로 자전축의 방향이 변하고, 천구의 북극[1]도 이동하게 된다. 이것이 북극성이 변화하는 원인이 된다.
여기서 지구의 세차운동은 자이로스코프나 팽이의 세차운동과 양상이 다르다.
파일:지구의 세차운동 원인.png
자이로스코프나 팽이의 경우 중력으로 인한 돌림힘이 '자전축을 쓰러뜨리는 방향'으로 작용한다. 하지만 지구는 반대다. 지구는 엄밀하게는 넙적한 타원체 모양을 하고 있기 때문에 위 그림과 같이 태양과 달 간의 인력을 받는다. 지구 기준으로 볼 때 나타나는 관성력인 원심력을 감안할 때, 힘의 크기는 (가까운 쪽의 인력)>원심력>(먼 쪽의 인력) 순으로 나타나 그림의 오른쪽과 같이 합력이 나타난다. 결국 알짜 돌림힘은 자전축을 똑바로 세우는 방향으로 나타난다. 이는 전술한 수식에서 [math] \vec{\tau} [/math] 의 방향이 반대로 나타남을 뜻한다.
참고로 위 그림은 외부 천체가 하지점에 왔을 때의 영향이다. 춘분점이나 추분점에서는 돌림힘이 상쇄가 되지만 하지점이나 동지점에서는 자전축을 세우는 작용이 최대로 나타난다. 평균적으로 볼 때, 태양과 달의 영향은 지구의 자전축을 세우려 한다.
이런 이유로 지구는 자전 방향과 세차운동 방향이 반대이다. 지구의 세차운동 주기는 약 25,800년이다. 황도의 북극에서 지구를 바라볼 때 자전 방향은 반시계, 세차운동은 시계방향이다. 지구의 세차운동 항목의 맨 위의 그림을 보면 반시계방향으로 그려져 있는데, 올바른 표시이다. 이는 황도의 남극에서 황도의 북극을 바라보는 시선이기 때문.
지구는 타원 궤도로 돌기 때문에 태양에 가장 가까운 근일점과 가장 먼 원일점이 생긴다. 이 때 세차운동으로 자전축 경사 방향이 변하면 근일점과 원일점에서의 계절도 바뀌게 된다.[2] 현재(2000년대) 북반구에서는 근일점(1월 4일경)에서 겨울, 원일점(7월 6일경)에서 여름이다. 세차운동으로 근일점에서 여름, 원일점에서 겨울이 되게 되면 여름은 더 더워지고 겨울은 더 추워진다. 즉, 북반구의 연평균 기온차가 커지게 된다. (남반구는 당연히 반대이다.