Stern–Gerlach experiment
1 개요
오토 슈테른(Otto Stern)과 발터 게를라흐(Walther Gerlach)가 1922년에 실시한 양자 역학 역사에서 중요한 실험 중 하나로, 초기 양자역학에서 제이만 효과(Zeeman Effect) 등과 함께 원자의 스핀의 존재를 밝혀낸 실험이자 그 스핀이 양자화돼있다는 사실을 밝혀낸 실험이다.
2 실험 내용
우선 진공에서 전기적으로 중성인 은[1]을 기화시켜서, 한 방향으로 정렬시켜 은 원자 빔을 만든다. 그리고 그렇게 생성된 은 원자 빔을 위와 같은 불균일한 자기장[2]을 통과시켜서, 자기장을 통과한 은 원자들이 건너편 스크린에 향하게 한다. 그렇게 반대쪽 스크린에 나온 은 원자들의 분포를 조사하면, 은 원자의 자기 모멘트 분포도 알 수 있는 실험이다.[3]
고전적으로 봤을 때는, 자기모멘트는 연속적인 값을 취할 수 있으므로, 예상되는 은 원자의 분포는 당연히 연속적인 분포를 보여야 된다. 그런데 실제 실험을 해보면, 연속적이긴 커녕 꼴랑 두 줄에 걸쳐서 은 원자가 검출되었다. 즉, 자기 모멘트가 연속적인 값이 아닌 딱 2개의 값만을 갖는다는 결과가 나와버린 것이다!
이에 물리학자들은 '뭔가 원자 자체의 각운동량이랑은 다른, 자기 모멘트를 만들어내는 무언가 다른 원인이 있지 않을까?'라는 생각을 가지게 되었고, 후에 이는 제이만 효과 실험과 함께 스핀이라는 개념으로 정립된다.
3 추가 실험
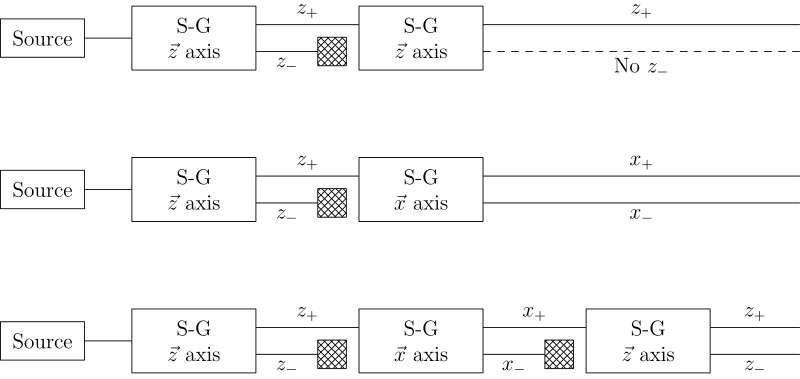
이 실험은 여기서 끝나지 않고 다음과 같은 실험으로 확장된다. 먼저, 위 실험에서 은 원자들이 '두 분류로 나뉘는' 현상을 확인했으므로, z축 방향으로 휘게 만드는 자기장을 만들어서 은 원자 빔을 통과시킨 후, 그 중에서 +z 방향으로 휜 은 원자 빔만을 다시 z축 방향으로 휘게 만드는 자기장에 통과시켰을 때는 은 원자는 +z 방향의 한 줄에서만 검출이 된다. 이는 이미 -z축 방향으로 휘어진 원자들은 다 '걸러냈으므로', +z축 방향으로만 원자가 휜다고 생각하면 문제가 없어보인다.
이번에는, z축방향 자기장 > 그 중 +z 방향 은 원자 빔 > x축 방향 자기장의 순서로 빔을 통과시켜 보자. 그러면 은 원자는 +x, -x 방향의 두 줄에서 검출이 된다. 고전 물리학적인 관점으로 생각했을 때, x축 방향 자기 모멘트, y축 방향 자기 모멘트, z축 방향 자기 모멘트가 전부 독립적으로 존재해서 +z축 방향으로 걸러낸 원자들 안에서도 +x축, -x축 방향 자기 모멘트가 존재한다고 생각하면 아무런 문제가 없다. 아직까지는.
마지막으로, z축방향 자기장 > 그 중 +z 방향 은 원자 빔 > x축 방향 자기장> 그 중 +x 방향 은 원자 빔 > z축방향 자기장에 다시 통과시킨다. 이 때 검출되는 은 원자는 몇 줄일까? 상식적으로 생각해보면 이미 -z축 방향으로 휘어진 원자들은 다 걸러냈으므로, 다시 z축 방향 자기장에 통과시킨다 한들 -z축 방향으로는 원자들이 휘지 않을 게 당연한 것 같다. 그런데 실제 실험을 해보면, +z축, -z축 방향의 원자가 두 줄로 분명히 검출된다! 이미 -z축 방향으로 휜 원자들을 '걸러냈음에도' 불구하고, 이런 결과가 나온 것이다.
이는 당연히 고전역학적인 결과로 설명할 수 없고, 양자 역학의 기묘한 특징 중 하나이자 그 난해함(...)을 대표적으로 나타내는 실험 중 하나이다. 이 현상은 불확정성 원리[4]와 양자역학의 관측에 관한 문제와도 관련이 있는 현상이다.
4 관련 문서
- ↑ 은을 사용한 이유는, 은이 굉장히 무거운 원자라 로렌츠 힘등의 다른 힘들의 효과를 적게 받고, 궤도 각운동량의 합이 0인 점, 그리고 (상대적으로) 큰 원자라 원자의 궤적을 고전역학적으로 기술해도 큰 탈이 없는 점 등 다양한 이점들 때문이다. 물론 이 실험 설계 당시엔 이런 점들을 전부 고려하진 않았을 테지만...
- ↑ 불균일한 자기장을 쓰는 이유는, 균일한 자기장에서 진행하는 자기 모멘트는 단순히 세차운동만을 일으키면서 진행 방향이 바뀌지 않지만, 적절히 잘 설계된 불균일한 자기장을 이용하면 진행 방향 자체를 특정 방향으로 휘게 만들 수 있다.
- ↑ [math]\vec F = (\vec m \cdot \vec \nabla) \vec B[/math]이므로, 은 원자가 자기장이 0일 때 검출되는 지점으로부터 얼마나 떨어져 있는지를 측정하면 자기 모멘트의 값도 역산할 수 있다.
- ↑ 수학적으로 말하면, z축 방향 스핀 연산자와 x축 방향 스핀 연산자가 비가환이라서 그런다. 수식으로 쓰면 [math][S_{z}, S_{x}] = i\hbar S_{y} \neq 0[/math]으로 나타내어지는데... 더 자세히 알고 싶으면 양자역학 교재를 참고하자.