한붓그리기

1 개요

500px-K%C3%B6nigsberg_graph.svg.png
[1]

한 번 지나간 선으로는 지나가지 않고 모든 선을 이어 그림을 완성하는 것. 붓을 종이에서 떼지 않고 한 번에 그린다고 해서 '한붓그리기'라는 이름이 붙었다.
이산수학에서는 경로가 닫혀있느냐[2] 아니냐에 따라 오일러 트레일(Euler trail), 또는 오일러 회로(Euler circuit)이라고 부른다.
우체부[3]가 쾨니히스베르크[4]에 있는 7개의 다리를 단 한 번씩만 건너서 다시 출발점으로 되돌아올 수 있겠냐는 문제를 1736년에 레온하르트 오일러가 그런 거 없다라고 증명한 것을 한붓그리기의 이론적 출발점으로 보고 있다.

2 한붓그리기가 가능하려면?

2015년 기준 고등학교 3학년까지는 '행렬과 그래프' 단원에서 한붓그리기가 가능한 그래프에 대해 배운다. 다만 새 교육과정을 적용받는 고1, 고2부터는 행렬 단원 자체가 아예 빠져서 더 이상 한붓그리기에 대해 배우지 못한다.
먼저 각 꼭짓점에 연결된 변의 개수를 그 꼭짓점의 차수라고 정의하면 한붓그리기가 가능한지 아닌지를 판단할 수 있다. 다음 두 가지 경우 중 하나이면 된다.

2.1 그래프의 꼭짓점의 차수가 모두 짝수

파일:Euler trail 01.png
이 경우에는 어떤 점에서 출발해도 다시 출발점으로 되돌아올 수 있다. 즉, 오일러 회로가 존재한다.
대표적인 그래프로 흔히 그리는 꼭짓점 5개짜리 별 그림이 있다.[5]

2.2 꼭짓점 딱 2개의 차수만 홀수이고 나머지는 모두 짝수

파일:Euler trail 02.png
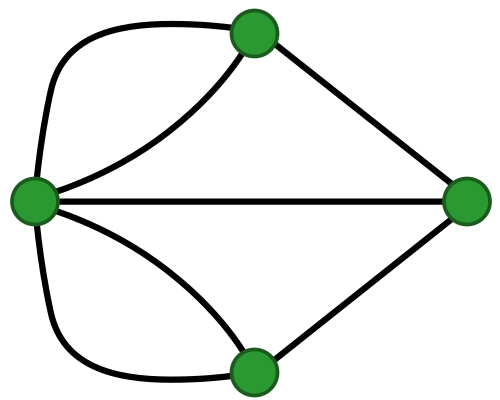
차수가 홀수인 점이 A와 B라고 했을 때, A에서 출발하면 B로 도착하게 된다. 즉, 오일러 트레일은 존재하지만 오일러 회로는 존재하지 않는다.
위 그림에서 하단의 3에서 출발하면 반대편 3으로 도착하게 되는 것을 알 수 있다.

3 게임

머리를 써야하는 퍼즐이기 때문에 여러 게임에서도 한붓그리기를 사용한다.

3.1 한붓그리기 게임목록

  1. ↑ 한붓그리기가 불가능한 것으로 유명한 '쾨니히스베르크 다리 건너기 문제'를 그래프로 도식화한 것.
  2. ↑ 출발점으로 다시 되돌아오면 닫힌 경로라고 한다.
  3. ↑ 정확히 우체부인지는 불명. 확인 후 수정바람.
  4. ↑ 지금은 러시아의 칼리닌그라드
  5. ↑ 꼭짓점 6개짜리 별인 육망성은 한붓그리기가 불가능하다. 하지만 각 변의 교차점에도 점을 찍어서 꼭짓점을 12개로 만들면 한붓그리기가 가능하다.