레인보우 테이블

1 설명

레인보우 테이블은 해시 함수(MD5, SHA-1, SHA-2 등)을 사용하여 만들어낼 수 있는 값들을 왕창 저장한 표이다. 물론 해시 함수는 입력이 무제한이라서 모든 내용을 넣는 게 아니고, 이를테면 영어 소문자와 숫자 조합으로 일정 길이까지의 모든 문자열에 대해서 계산한다거나, 하는 것이다. 이걸 그대로 저장하면 거듭제곱의 위력을 확실하게 체험할 수 있기 때문에 (문자열에 한 글자 추가하면 아무리 적어도 30배, 문자 조합이 많으면 200배 정도로 커진다!) 적절한 가공 과정을 거친다. 이건 후술.

이렇게 무식하게 값을 때려박는 테이블의 특성상, 작은 테이블도 기본 100GB는 거뜬히 넘어주신다. 영어 대문자+소문자+숫자 조합까지 가면 완전히 헬게이트. 올라가는 것도 테라바이트 단위로 용량이 커진다. 이러한 특성 때문에 기업, 단체에서 주로 사용한다. 개인이 사용하기엔 자원이 너무나도 많이 들어가 어느정도 돈이 많지 않은 이상 힘들기 때문이다.

2 만들어진 이유

만들어진 이유는 여러가지가 있다.

2.1 브루트 포스 공격시 더 빠르게 비밀번호를 시도해 보기 위해서

브루트 포스 항목에도 나와 있듯이, 무식하게 대입을 하는 데에는 시간이 엄청나게 걸린다. 10자리 영문 소문자+숫자 조합을 초당 1억번 대입을 한다 하더라도 1년 이상 걸리는데, 해쉬를 계산하느라 초당 대입량이 적어지면... 이러한 문제를 조금이나마 해결하기 위해 나온 것이 첫 번째 이유이다. 해쉬를 일일히 계산해 내느니 차라리 미리 만들어진 테이블에서 해쉬값만 쏙쏙 뽑아다가 집어넣으면 해쉬 계산하는 시간이 절약되니 공격 과정을 좀 더 빨리 끝낼 수 있다. 일종의 사전 공격.

2.2 해쉬에서 평문을 추출해내기 위해서

해쉬는 기본적으로 역함수가 존재하지 않는 함수로 계산해낸다. 즉, 암호화-복호화 과정이 불가능하다는 말이다. 그래서 ~~할일 없는~~ 사람들이 고안해낸 방법은 수학적으로 아예 역함수가 존재하지 않는 함수 가지고 씨름할 바에 차라리 가능한 모든 경우의 수를 다 써놓고 거기서 찾아내자!이다. 그래서 데이터베이스와 같은 자료에서 뽑아낸 해쉬값을 레인보우 테이블과 대조하여 평문을 찾아내는 것이다.

3 아이디어

그냥 가능한 모든 값들을 저장하면 되는 걸 굳이 왜 "레인보우 테이블"이라고 부르냐 하면, 레인보우 테이블은 계산 시간을 희생해서 공간을 압도적으로 줄일 수 있다. 이를테면 암호 하나를 찾는 시간을 10만배 늘리는 대신 테이블을 10만분의 1로 줄일 수 있는 것. 어차피 해시 함수는 10만배 느려져 봤자 밀리초 단위기도 하고, 레인보우 테이블에 저장되는 값 숫자 대비 찾을 암호 숫자가 매우 적기 때문에 쓸만한 것이다.

(원 이미지, CC-by-sa 2.5로 배포됨)

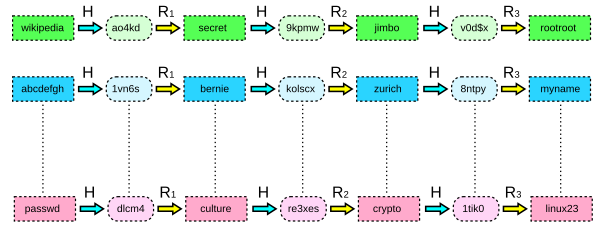
레인보우 테이블에는 해시 함수 H 말고도 이 해시의 결과를 레인보우 테이블의 가능한 입력으로 변환해 주는 함수 R이 더 들어간다. 물론 R은 입력에 따라 다르고, 해시 함수와는 달리 원래 가능한 입력에 적절히 대응만 되기만 하면 된다. 다르게 생각하면, 레인보우 테이블은 H를 깨는 게 아니라 f(x) = R(H(x))인 f를 깬다. H와는 달리 f는 입력과 출력이 같기 때문에 다루기가 쉽다.

처음에 테이블을 만들 때는...

가능한 입력 중 하나를 잡아서 H를 적용한다.
함수의 결과를 R로 변환한다.
이 과정을 필요한 숫자(k회라고 하자)만큼 반복한다.
이제 입력 x와 마지막에 변환된 값 y = R(H(...R(H(x))...)) = f^k(x)를 저장한다.
이 작업을 최대한 많은 입력에 대해 반복한다.

여기서 중요한 점은, x와 y만 저장해도 계산만 좀 더 하면 f(x), f(f(x)), ..., f^k-1(x)의 다른 k-1개의 입력이 커버된다는 것이다. 중간에 저장해야 할 게 k개에서 1개가 되었으니 공간이 1/k가 된다!

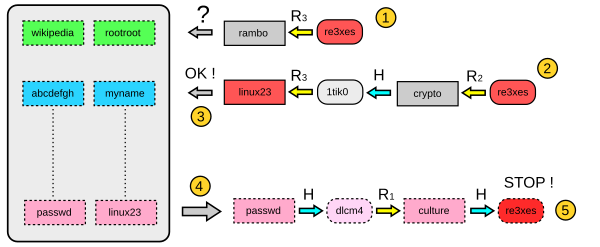
이 테이블을 써 먹으려면, 입력 a = H(b)가 있을 때 R(a), R(H(R(a))), ...를 계산해서 테이블의 y에 겹치는 게 있는지 보면 된다. 겹치는 게 있다면 대응되는 x로부터 최대 k번 f를 적용해서 b가 나오는지 확인해 보면 된다. (f(b) = f(c)인 c가 있을 수 있으므로 확인이 실패할 수 있다.) 안 나오면 그냥 한 번도 커버가 안 된 거고 나오면 잘 된 거다. 참 쉽죠?

...실은 뻥이고, 이 방법은 치명적인 문제가 있는데 입력이 많이 들어가면 많이 들어갈 수록 f(x), f(f(x)) 등이 서로 충돌할 가능성이 높아진다. 한 번 충돌이 나는 입력이 나오면 거기서부터는 커버되는 입력들이 똑같으니까 공간 절약이 1/k에서 확 줄어들 수 있는데, 이런 (x, y) 쌍들을 걸러낼 수 없다! 예를 들어 "뿌뿌뽕"을 f에 세 번 돌린 것과 "용개"를 f에 다섯 번 돌린 게 같은 값이 나온다고 하자. 그러면 이 두 값이 커버하는 입력의 개수는 2k개가 아니라 k+5개^[1] 밖에 안 되니까 도움이 안 된다. 이럴 바에는 둘 중 하나를 날려 버리면 좋겠는데 (x, y) 쌍만 가지고는 이걸 알 수 없다.