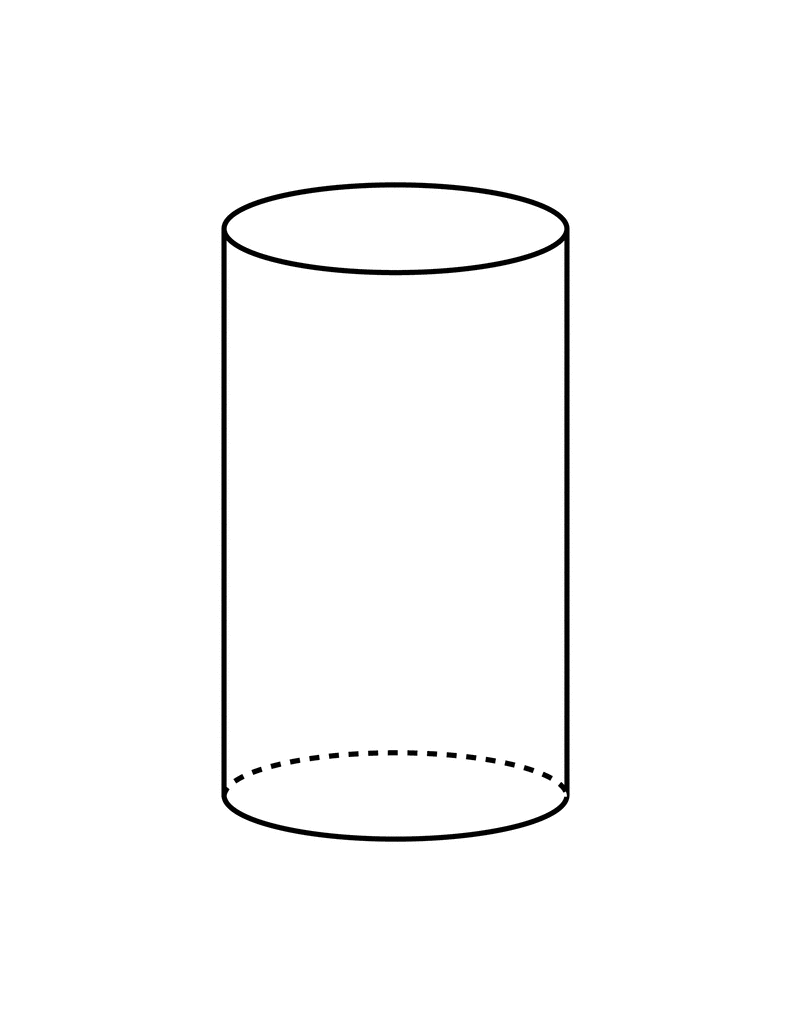
1 개요
이름 그대로 밑면이 원인 기둥이다. 원통이라고도 한다. 엄밀하게는 밑면과 윗면이 서로 평행한 합동 관계의 두 원이고[1], 밑면의 원주 위의 점을 윗면의 원주 위의 가장 가까운 점을 이은 무수히 많은 선들을 포함한 3차원의 입체도형. 이때 이 선들로 생긴 부분이 원기둥의 옆면이다.
2 본문
보통 교과서에는 위 그림과 같이 직사각형을 회전시킨 직원기둥 만을 다룬다. 공식도 당연히 직원기둥에만 적용되는 것. 하지만 원뿔과 마찬가지로 모든 원기둥이 직원기둥일 필요는 없으며, 윗면과 밑면이 수직 위아래로 있지 않고 살짝 비껴가 있으면 빗원기둥이 된다.
직원기둥의 높이를 [math]h[/math], 반지름을 [math]r[/math]라고 할 때, 부피는 [math]\pi r^2h[/math]이고, 겉넓이는 [math]2\pi r^2+2\pi rh = 2\pi r (r+h)[/math]이다. 더 쉽게 말하자면 밑넓이 × 높이가 부피. 밑넓이 × 2 + 옆면의 넓이가 겉넓이이다. 인수분해한 것과 같이 원둘레 × (반지름 + 높이)로 계산해도 같은 결과가 나온다.
빗원기둥은... 답이 없다(...). 적분만이 해결책.
3 여담
좌표계 중에 원기둥 형태의 좌표계가 있는데, 반지름과 각도와 높이([math]r, \theta, z[/math])로 구성된다. HSB 색좌표가 실 사용 예 중 하나.
정육면체, 구와 함께 미술 소묘할 때의 기본적인 도형이다.
통나무집은 대부분 이렇게 생긴 나무를 쌓아서 만든다.