목차
1 개요
作圖, Construction. 그림, 설계도, 지도 따위를 그리는 일.
수학적인 의미로는 주어진 조건에 알맞은 도형을 그리는 일을 말한다. 고대 그리스인들은 자와 컴퍼스만으로 그릴 수 있는 형태, 즉 원과 직선을 가장 기본적이고, 예술적인 기하도형으로 생각했다. 그래서 그것들의 조합으로 기하학적 도형을 그리는 방법을 연구하였고, 그래서 자와 컴퍼스만으로 임의의 도형을 그리는 방법을 연구하였으며, 다른 도구는 사용하기를 꺼려하였다. 즉, 그리스인이 생각한 컴퍼스와 눈금없는 자를 유클리드 도구라고 부르는데, 이것으로 도형을 그리는 것을 작도라고 부른다.
2 유클리드 도구와 작도의 다양한 도구들
그리스인이 생각한 컴퍼스와 눈금없는 자를 유클리드 도구라고 부른다. 고전기하학에서 작도란 이 두 도구만을 사용해서 도형을 그리는 유클리드 작도[1]를 말한다. 그런데 유클리드도구에서 눈금없는 자는 두 점을 잇는 선분을 그리는 도구라서 현재와 같은데, 컴퍼스는 주어진 한 점을 중심으로 하고 또 다른 주어진 한 점을 지나는 원을 그리는 도구라서, 현재의 선분을 옮길 수 있는 컴퍼스와는 약간 다르다. 즉, 현재의 컴퍼스는 "유클리드 컴퍼스+디바인더"인셈. 이런 유클리드 컴퍼스대신 현재의 컴퍼스를 쓸 수 있는 이유는, 둘의 기능이 동등하다는 컴퍼스 동등정리 덕분이다.
참고로 모르-마스케로니 정리에 의해서 유클리드 작도 가능한 도형은 컴퍼스만으로도 작도 가능하고[2], 퐁슬레-슈타이너 정리에 의해서 유클리드 작도 가능한 도형은 중심을 알고 있는 호 하나랑 눈금없는 자만으로 작도 가능하다[3].
2.1 작도의 예
2.1.1 임의의 각 2등분하기

- 두 반직선의 교점을 중심으로 해서 두 반직선을 지나는 호를 그린다.
- 위 1번의 호와 반직선의 교점을 중심으로 호를 하나씩 그린다. 양쪽 호의 반지름 길이는 서로 같아야 하며 두 호가 서로 만나도록 해야 한다.
- 위 1번의 두 반직선의 교점을 출발해 위 2번의 두 호의 교점을 지나는 반직선을 그리면 각이 2등분된다.
2.1.2 선분의 수직2등분선 그리기[4]

- 선분의 양 끝을 중심으로 해서 호를 그린다. 단, 호의 반지름은 선분의 길이를 반으로 나눈 것보다 더 길어야 하고 두 호의 교점이 두 개 생기도록 그려야 한다.
- 위 1번의 두 호의 교점 두 개를 이으면 수직2등분선이 된다.
2.1.3 원과 내접하는 정삼각형 그리기

- 직선을 그린 후 그 직선 위에 중심을 잡고 적당한 크기의 원을 그린다.
- 컴퍼스의 지름은 그대로 두고 위 1번의 직선과 원의 교점 중 하나를 골라서 그 점을 중심으로 호를 그린다. 여기서 원과 호의 교점은 두 개가 생기도록 해야 한다.
- 원과 위 2번의 호의 교점 두 개를 끝으로 하는 선분을 그린다. 이 두 끝이 정삼각형의 두 꼭지점이 될 것이다.
- 나머지 한 점은 위 2번의 교점 중 반대쪽과 연결하면 정삼각형이 된다.
2.2 작도할 수 없는 도형
눈금 없는 자와 컴퍼스를 이용하면 많은 도형을 작도할 수 있지만, 도구가 제한적인만큼 작도할 수 없는 도형도 많다. 대표적인 예로 다음과 같은 3가지 문제들이 있다.
- 주어진 임의의 각을 3등분하는 문제
- 주어진 정육면체의 2배의 부피를 갖는 정육면체를 작도하는 문제
- 주어진 원과 면적이 같은 정사각형을 작도하는 문제
예로부터 이 3가지 문제를 풀기 위해 여러 시도가 있었으나, 오랜 연구를 거친 결과 작도가 불가능함이 증명되었다. 3대 작도 불능 문제 참조.
2.3 작도 가능한 정다각형
정다각형의 경우 작도가 가능한 정다각형이 있고 그렇지 않은 정다각형이 있다. 정삼각형, 정사각형, 정오각형은 모두 작도 가능하므로 3, 4, 5의 2배수 혹은 2의 거듭제곱(2^n) 배수 각형들은 모두 작도 가능하다는 사실은 쉽게 알 수 있다. 또한 페르마 소수 (Fn = 2^2^n + 1 형태의 소수)만큼의 변을 가진 정다각형도 작도 가능하다. 즉, 페르마 소수인 17, 257, 65537각형은 모두 작도 가능하다는 이야기이다. 유명한 수학자인 가우스가 정17각형이 작도 가능하다는 사실을 대학생 시절에 발견했다는 것은 꽤 유명한 이야기. 단, 작도 가능하다는 사실만 증명했고 실제 작도법을 이 때 찾아낸 것은 아니다. 실제 작도법은 이보다 훨씬 늦게 나왔다. # 5개의 페르마 소수 외에는 소수개의 변을 가진 정다각형은 무조건 작도 불가능하다.
정257각형의 작도법은 나왔으나, 정65537각형의 작도법은 아직 나오지 않았다[5].
더 깊게 들어가자면 정17각형으로부터 나오는 삼각함수 값에 대해서만 대수적인 표기 방법이 나왔고, 정257각형 [6]과 정65537각형으로부터 나오는 삼각함수 값도 대수적 수임이 증명되었는데, 그 표현법은 엄청나게 복잡하다. 한 예로 정17각형으로부터 유도되는 삼각함수 값 중 가장 간단히(!) 표현되는 것은 아래와 같다. 고만해 미친놈들아
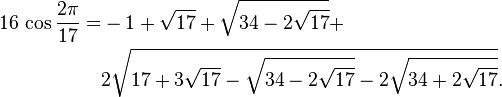
이를 이용하여 작도 가능한 각도를 얻을 수 있다.
2.4 3대 작도 불능 문제
항목 참조
2.5 기타
정칠각형은 7이 페르마 소수에 들어가지 않기 때문에 일반적인 작도법으로는 작도할 수 없지만, 눈금이 있는 자의 사용을 허용하는 '뉴시스(Neusis) 작도법'으로는 가능하다.
자와 컴퍼스 대신 종이접기를 이용한 작도를 사용하면 3대 작도 불능 문제 중 앞의 2개를 풀 수 있다. 종이접기 작도 참조. 뉴시스 작도법과 작도할 수 있는 범위가 같다.