콘웨이의 생명 게임

1 개요

Gospers_glider_gun.gif
이 패턴은 글라이더를 계속 양산하며 무한히 반복되는 패턴 중 하나인 가스퍼의 글라이더 건(Gosper's Glider Gun). 화면이 이어져 있지 않은 이상 완전 무한 반복이 된다.

Conway's Game of Life.[1] 영국의 수학자 존 호튼 콘웨이가 고안해낸 세포 자동자 게임. 바둑판처럼 정사각형의 여러 칸으로 나뉘어진 공간에서 한 칸에 한 마리씩 있는 세포들의 삶과 죽음이 펼쳐지는 게임이다. 말이 게임이지 실제로는 게임자가 처음 세포들의 위치를 입력하면 그 규칙에 따라 삶과 죽음이 일어나는 것을 재미있게 구경(…)하면 된다.

규칙은 단순하지만 만들어 낼 수 있는 패턴이 무수히 많아서 관심을 끈 게임이기도 하며, 컴퓨터 과학에서도 다루고 있는 게임이다.

2 규칙

다음 세대로 넘어갈 때 세포들의 생사가 결정되는데, 인접한 8개의 칸을 기준으로 하며 그 기준은 다음과 같다.

  • 어떤 칸과 인접한 8칸 중 정확히 3칸에 세포가 살아 있다면 해당 칸의 세포는 그 다음 세대에 살 수 있다. (계속 살아 있거나 죽은 상태에서 살아난다.)
  • 어떤 칸과 인접한 8칸 중 정확히 2칸에 세포가 살아 있다면 해당 칸의 세포는 살아 있는 상태 혹은 죽은 상태를 계속 유지한다.
  • 그 이외의 경우 [2] 해당 칸의 세포는 다음 세대에 고립돼 죽거나 혹은 주위가 너무 복잡해져서 죽는다. (계속 죽어 있거나 이미 살아 있는 상태라면 죽는다.)

즉, 표로 정리하면 다음과 같다.

구분인접 세포 수
칸 구분1 이하234 이상
세포가 살아있는 칸OFFONONOFF
세포가 죽은 칸OFFOFFONOFF

이 표에서 ON은 다음 세대에 그 자리의 세포가 삶을, OFF는 다음 세대에 그 자리의 세포가 죽음을 의미한다.

예를 들어, 세포 5마리가 다음과 같이 배열되어 있다고 하자.

파일:Attachment/conwaygame 5cross.png

이들의 생사 진행은 다음과 같다. 세포가 살아있는 칸에서 X표시는 다음 세대에 죽음을, 세포가 살아있지 않은 칸에서 O표시는 다음 세대에 살아남을 의미한다.

0123
파일:Attachment/conwaygame 5cross 0.png파일:Attachment/conwaygame 5cross 1.png파일:Attachment/conwaygame 5cross 2.png파일:Attachment/conwaygame 5cross 3.png
4567
파일:Attachment/conwaygame 5cross 4.png파일:Attachment/conwaygame 5cross 5.png파일:Attachment/conwaygame 5cross 6.png파일:Attachment/conwaygame 5cross 7.png
8(6)9(7)10(6)11(7)
파일:Attachment/conwaygame 5cross 6.png파일:Attachment/conwaygame 5cross 7.png파일:Attachment/conwaygame 5cross 6.png파일:Attachment/conwaygame 5cross 7.png

제1세대부터 제7세대까지 진행되다가 제8세대 이후는 제6세대와 제7세대의 패턴이 무한히 반복된다.

또한 주변에 3개의 세포가 살아있을 때 태어나고 주변에 2, 3개의 세포가 살아있을 때 생존하므로 이를 B3/S23 과 같이 표기한다.
이때 B는 탄생(Birth)을, S는 생존(Survive)을 뜻한다.

3 패턴

다양한 패턴이 존재한다.

3.1 무한 패턴

결국에는 모든 세포가 죽어버리는 패턴이 존재하는가하면, 세포가 전멸하지 않고 영원히 살아남거나 생사가 무한히 반복되는 영구 패턴이 존재한다.

적은 수의 세포 배열이 무한 패턴을 형성하는 예는 다음과 같다. 이 패턴은 외부 패턴과 충돌하지 않는 이상 무한으로 반복된다.

최소한의 세포로 무한 패턴이 가능한 세포 숫자는 3이며, 정물 패턴이 가능한 최소한의 세포 숫자는 4이다.

3.1.1 정물 (Still Lifes)

세포들이 서로를 살려서 불로불사 죽지도 않고 살아나지도 않고 계속 멈춰있는 형태다.

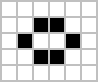66px-Game_of_life_block_with_border.svg.png98px-Game_of_life_beehive.svg.png98px-Game_of_life_loaf.svg.png82px-Game_of_life_boat.svg.png
블록벌집빵덩이나이스 보트

3.1.2 진동자 (Oscillators)

정물과는 다르게 세포들 중 일부만 영원히 살아있고 나머지는 그 자리에서 삶과 죽음을 무한히 반복하는 형태다. 다만, 영원히 살아있는 세포가 없는 진동자도 존재한다. 진동자에서 영원히 살아있는 세포를 고정자(stator)라고 하고 삶과 죽음을 반복하는 세포를 회전자(rotor)라고 한다. 회전자만으로 이루어진 진동자를 부르는 명칭은 strictly volatile oscillator이다.(번역은 추가바람) 그리고 회전자만으로 이루어진 주기 3인 진동자가 2012년에 발견되었다. 반면, 불사조의 조건은 이것보다 훨씬 까다로운데, 진동자의 한 주기 내의 모든 세대에서 살아 있는 세포는 다음 세대에 전멸해야 한다. (대신 다음 세대에 새로운 세포가 탄생하면서 진동자를 유지시킨다.) 주기가 2인 불사조는 예전부터 알려져 있었고, 주기가 3인 불사조는 존재하지 않음이 증명되어 있지만, 주기가 4 이상인 불사조가 존재하는지는 알려져 있지 않다. 아래 표에서 괄호 안의 숫자는 반복 주기. 즉, 몇 세대 만에 원래 패턴으로 돌아오는지 적어 놓은 것이다.

Game_of_life_blinker.gifGame_of_life_toad.gifGame_of_life_beacon.gifGame_of_life_pulsar.gif
깜빡이 (2)두꺼비 (2)등대 (2)펄서 (3)

정물을 주기가 1인 진동자로 보기도 한다.
2014년 7월 현재까지 주기가 19, 23, 34, 38, 41인 진동자는 발견되지 않았다. 주기가 34인 진동자는 주기가 2인 진동자와 주기가 17인 진동자를 적절히 조합하면 만들어 낼 수 있다. 그러나 34의 주기를 가지고 진동하는 세포가 없기에 따지지 않는다. 이런 경우를 '자명한'(trivial) 해(解)라고 한다.

3.1.3 우주선 (Spaceships)

계속 전진하는 패턴을 말한다. 다시 말해서, 세포들이 자리를 이동하면서 생사가 무한히 반복되는 패턴.

Game_of_life_animated_glider.gifGame_of_life_animated_LWSS.gif
글라이더경량 우주선 (LWSS)

글라이더는 대각선으로, 경량 우주선은 수직 또는 수평으로 움직인다. 저 앞의 개요에서 리젠되는 녀석들이 바로 글라이더다.
우주선마다 각자의 속도(veloity)가 있다. 속도는 패턴이 몇을 주기로 반복되는가와, 한 주기동안 얼마나 이동하는가에 따라 측정하는데, y의 주기동안 x칸만큼 이동하면 xc/y라고 표기한다. (c는 1세대당 1칸 이동하는 속도로, 생명 게임에서 정보가 이동할 수 있는 최대 속도여서 빛의 속도를 나타내는 c로 표기한다. x와 y가 서로소가 아닐 경우 약분할 수 있다.) 2016년 3월 현재 발견된 우주선의 속도는 수직수평으로 움직이는 것이 c/2, 3c/7, c/3, c/4, c/5, 2c/5, c/6, c/7, 2c/7, 17c/45, 31c/240, c/10이 있으며, 대각선으로 움직이는 것이 c/4, c/5, c/6, c/7, c/12이 있다. 속도를 더욱 명확히 하기 위해 가로로 움직인 거리와 세로로 움직인 거리를 따로 적어주는 경우도 있다. (5120,1024)c/33699586 이런 식으로.[3]

3.1.4 특수한 무한 패턴들

  • 총 (gun): 한 자리에서 패턴을 무한히 반복하면서 우주선을 계속 생성한다. 개요에 나온 가스퍼의 글라이더 건(Gosper's Glider Gun)이 대표적인 예.
  • 미끄럼총 (slidegun): 총과 비슷하나, 우주선의 궤적을 한쪽으로 조금씩 밀면서 쏜다.
  • 기관차 (puffer): 패턴을 남기면서 계속 전진한다.
  • 갈퀴 (rake): 기관차의 특수한 경우로 남기는 패턴이 모두 우주선인 경우다. [4]
  • 심지 (wick): 특정한 패턴이 길게 반복되어 진동자처럼 일정한 주기를 가지고 진동한다.
  • 심지늘이개 (wickscretcher): 기관차처럼 심지를 계속 늘린다.
  • 한천 (Agar.io): 심지의 2차원 버전이라고 할 수 있다.
  • 우주채우개 (spacefiller): 한전을 사방으로 계속 늘린다.
  • 사육사 (breeder): 기관차와 비슷하나, 패턴이 2차원적으로 퍼진다.
사육사는 또 다시 4가지로 분류된다.
MMS: 갈퀴가 기관차를 뿌리는 경우.
MSM: 기관차가 총을 뿌리는 경우.
SMM: 총이 갈퀴를 뿌리는 경우.
MMM: 갈퀴가 갈퀴를 뿌리는 경우.
가끔식 우주채우개도 사육사로 쳐 주는 경우도 있으며, 미끄럼총을 이용하면 MSS나 SSS등도 만들 수 있다.

3.2 장수 (Methuselah)

세포들이 전멸하거나 진동자에 수렴하는 상태를 안정화라고 하는데, 이 안정화에 이르기까지 오랜 세대를 요하는 패턴을 장수 패턴이라고 부른다. 영어 명칭은 므두셀라의 이름을 땄다.

아래는 몇 가지 장수 패턴들의 예

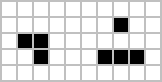82px-Game_of_life_fpento.svg.png162px-Game_of_life_diehard.svg.png146px-Game_of_life_acorn.svg.png
R-펜토미노다이하드도토리

R-펜토미노를 보면 알겠지만 세포 수는 불과 다섯인데도 의외로 번식력이 질기다. 다이하드와 도토리도 겨우 7개뿐인 세포가 보기에는 단명할 것 같은데도 실제로 해보면 엄청난 번식력을 자랑한다.

참고로, 화면 끝이 반대쪽과 서로 연결된 경우 안정화가 된 뒤에도 남아있는 우주선이 정물이나 진동자를 건드려 불안정한 패턴이 다시 이어지는 일도 있다. 특정 모양의 경우 남아있는 정물과 진동자가 워낙에 많아서 무려 3만 5천 세대나 가서야 겨우 완전히 안정화되는 사례도 있다.

3.3 무한 성장 패턴

반복 패턴 없이 성장을 무한히 반복해나가는 패턴이다.

162px-Game_of_life_infinite1.svg.png2x12_infinite.png
최소 세포로 무한 성장 (10)최소 면적으로 무한 성장 (2x12)[5]
329px-Game_of_life_infinite3.svg.png
두께가 1인 무한 성장

4 그 외

수십 년 동안 사람들이 취미로파 오던 분야라서 정신나간 생명이 꽤 많다.

  • 메타픽셀. 이게 뭐하는 것이냐면... 몰라 뭐야 이거 엄청 무서워
  • 소수(Prime) 번째 우주선만 내보내고 나머지는 먹어버리는 프라이머(Primer). 조금 응용하면 쌍둥이 소수만 내보내거나 페르마 소수만 내보낼 수도 있다.
  • 충분히 큰(49 이상) 주기의 글라이더 건 및 진동자를 모두 만들 수 있게 해 주는 허셜 회로
  • 튜링 머신. 이걸 좀 응용하면 수학적 상수 계산도 가능하다.
  • 한 줄 짜리 이차함수적으로 성장하는 생명 및 23개[6]짜리 이차함수적으로 성장하는 생명
  • 다양한 속도의 우주선. 270세대마다 102칸을 나가는 천만 개짜리 애벌레(Catepillar)와 자신을 만들고, 제거하면서 33699586세대마다 (5120,1024)칸만큼 이동하는, 수백만 칸에 걸쳐 있는 쌍둥이(Gemini)가 좋은 예.
  • 2016년 4월 현재 Caterloopillar라는 우주선이 제작되었는데, 이 방식을 이용하면 c/4 미만의 속도를 가진 수직, 수평방향으로 이동하는 우주선을 모두 만들수 있다.

검색어로 이스터 에그를 만들기로 유명한 구글의 검색창에 "Conway's Game of Life"라고 쳐 보면, 규칙에 따라 삶과 죽음을 반복하는 세포들이 화면을 아름답게(?) 수놓을 것이다.
울프람알파의 로딩 화면도 이 라이프게임으로 되어 있다.

파우더토이에서 Game Of Life 칸을 클릭하면 이 게임을 해볼 수 있는 픽셀들이 있다. 픽셀 들마다 성질이 다르며 전투력/생명력 같은게 있어서 서로 정복 전쟁을 한다.(...)

2016학년도 경찰대학 수학 영역으로도 출제되었다.
  1. ↑ 그냥 Game of Life는 인생게임.
  2. ↑ 즉 어떤 칸과 인접한 8칸 중에 살아 있는 세포의 개수가 0, 1, 4, 5, 6, 7, 8개일 경우
  3. ↑ 쌍둥이자리(Gemini)의 속도다.
  4. ↑ 그런데 남기는 패턴에 우주선이 포함되기만 해도 갈퀴로 쳐주는 경우도 있다.
  5. ↑ 2009년까지는 5x5였는데 경신됐다.
  6. ↑ 26개가 8년 동안 최소 기록이었는데 2014년에 갱신되었다.