단진자

1 개요

단진자(Simple pendulum)는 고정된 점과 질점이 일정한 거리를 유지하면서 연직면 상에서 움직이는 진동자를 일컫는다. 단순조화운동과 관련하여 대표적으로 다루어지는 대상이다.

단진자의 원리를 활용한 물건 중 하나로 그네가 있다.

2 단진자의 운동

※이미지 출처. 이하 필요 시 교체 바람.

위 그림과 같이 실로 매달린 추가 중력을 받으며 왕복운동을 하고 있다. 실의 길이는 일정하므로 추의 위치는 기준선에서 떨어진 각도 하나로 나타낼 수 있다. 즉 운동의 자유도는 1이다.

질량이 [math] m [/math] 인 추가 길이 [math] l [/math] 인 실에 매달리며 [math] \theta [/math] 만큼 떨어져 있다고 하면, 운동방정식을 [math] \theta [/math] 에 관한 미분방정식으로 표현할 수 있다. 우선 중력을 연직 방향으로 [math] mg [/math] 만큼 받는데, 실질적으로 운동에 영향을 미치는 것은 원호 방향의 성분이다. (나머지 힘은 줄의 장력으로 상쇄된다.) 한편 각도 [math] \theta [/math] 만큼 떨어져 있을 때, 원호의 길이는 [math] l\theta [/math] 이다. 이를 종합하면 아래와 같은 방정식이 세워진다.

[math] \displaystyle m \ell\frac{d^{2}\theta}{dt^{2}}=-mg\sin\theta [/math]

[math]mg\sin\theta[/math] 를 좌변으로 옮겨 우변을 0으로 만들고, 적절한 팩터를 곱하면 다음과 같은 식이 된다.

[math] \displaystyle \frac{d^2 \theta}{dt^2} + \frac{g}{\ell} \sin\theta = 0[/math]

한편 중력이 보존력임을 이용하여 역학적 에너지 보존 법칙에서부터 출발하여 운동방정식을 얻는 방법도 있다. 최대 진폭 [math] \theta_0 [/math] 에서는 진자가 멈춰 있어야 하므로, 에너지 보존 식을 쓰면,

[math] \displaystyle T+V=\frac{1}{2} m \ell^{2}\left(\frac{d\theta}{dt}\right)^{2} -mg \ell\cos\theta=-mg \ell\cos\theta_{0} [/math]

와 같고, 이는 아래와 같이 정리할 수 있다.

[math] \displaystyle \frac{1}{2} \left(\frac{d\theta}{dt}\right)^{2}=\omega_{0}^{2}(\cos\theta-\cos\theta_{0}), \quad \omega_{0} \equiv \sqrt{g \over \ell} [/math]

2.1 근사적인 해

원 방정식은 바로 풀기에는 매우 곤란한 형태를 가지고 있으므로 대부분의 경우 단순조화운동 형태로 근사시킨다. 진폭이 매우 작다고 가정하고 사인 항을 다음과 같이 근사시키는 것이다.

[math]\displaystyle \sin\theta = \sum_{n=1}^{\infty} {\theta^{2n-1} \over (-1)^{1+n} (2n - 1)!} = \theta - {\theta^{3} \over 3!} + {\theta^{5} \over 5!} - \cdots \approx \theta [/math]

이러한 근사된 미분 방정식의 해는 조화함수(사인함수)이다. 가로 변위 [math] x [/math] 도 비슷하게 얻어진다.

[math] \displaystyle \theta=\theta_{0}\sin \left(\sqrt{g \over \ell}t+\phi \right) [/math]

[math]\displaystyle x=x_{0}\sin \left(\sqrt{g \over \ell}t+\phi \right), \quad x \approx \ell\theta [/math]

그리고 단진자의 주기는 위 사인함수의 주기이다.

[math] \displaystyle T=2\pi\sqrt{\ell \over g} [/math]

이 결과로부터 단진자의 주기는 추의 질량이나 진폭에 의존하지 않음을 알 수 있다.

2.2 근사적인 해의 신뢰도

위와 같이 얻은 해가 어디까지 유효한가를 살펴볼 필요가 있다. 아래 섹션의 정확한 풀이에서 나온 식을 대입하여 계산하면 아래 결과를 얻는다.
단, 진폭이 둔각인 경우 실을 막대와 같은 단단한 걸로 바꿔서 실이 느슨해지는 경우(장력이 음수가 되는 경우)를 없앴다고 가정한다. 오차율은 근사 식을 기준으로 얼마나 벗어나는지를 나타낸다.

진폭(deg)	실제 주기	진폭(deg)	실제 주기
5	+0.048%	75	+11.89%
10	+0.19%	90	+18.03%
15	+0.43%	120	+37.29%
20	+0.77%	150	+76.22%
30	+1.74%	175	+187.8%
45	+4.00%	179	+360.0%
60	+7.32%	180	(무한대)

대략 20도 범위에서 오차율을 1% 이내로 줄일 수 있다. 따라서 위의 근사를 별 다른 무리 없이 쓸 수 있다.

3 활용 예

진폭이 작은 상황에 한하여, 진자의 주기는 추의 질량이나 진폭에는 의존하지 않고 오로지 실의 길이에만 상관이 있음을 알 수 있다. 이를 이용하여 시계추의 주기를 추의 늘어진 거리를 조절함으로써 설정할 수 있다.

단진자운동은 진자 팔의 길이의 제곱근에 비례하는 거의 일정한 주기를 가지므로 최초의 근대적 시계나 괘종시계 등에 쓰였다. 통상 길이가 25 cm 정도면 주기가 1초, 1미터 가량이면 2초 정도이다. 진자의 팔 길이만 일정하고 진폭이 크지 않으면 ( x ≈ sin x ) 주기는 추의 무게에 상관없이 상당히 높은 시간 안정성을 가지므로 쿼츠 (수정발진자)가 보편화되기전에는 가정의 괘종시계는 주로 진자를 이용하였다. 괘종시계의 진자의 팔은 온도팽창계수가 매우 낮은 invar라는 니켈합금으로 만들어 온도의 영향을 최소화 한다. 그래도 통상 한달에 몇 분 정도는 오차가 있어서 한달에 한 번 정도는 시간을 맞춰 줘야 했다.

4 단진자의 변형

4.1 곡면 위의 운동

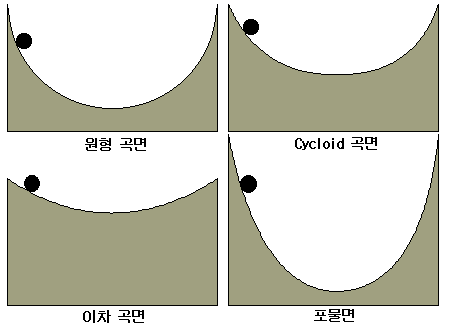
이미지 출처
위 그림과 같이 곡면 위를 왕복할 때에도 단진자의 모델로서 나타낼 수 있다. 실의 장력이 곡면의 수직항력으로 대치된다.
곡선마다 다르게 나타나지만 공통적으로 작은 진폭에 한하여 단진자의 운동처럼 기술할 수 있다.

가장 낮은 지점의 곡면의 곡률 [math] \eta [/math] 에 의존하여 진동한다. 즉 단진자의 경우 실의 길이가 [math] \ell [/math] 일 때 궤적의 곡률은 실의 길이의 역수이므로, 다음과 같은 식을 유추할 수 있다. 여기서 [math] x [/math] 는 가로 변위를 나타낸다.

[math] \displaystyle \eta = \ell^{-1} [/math]

[math] \displaystyle x=x_{0} \sin \left(\sqrt{g\eta} t+\phi \right), \quad T=\frac{2\pi} {\sqrt{g\eta}} [/math]

4.2 하위헌스의 진자시계

이미지 출처
그림에서 진자의 끝은 사이클로이드 모양으로 궤적을 그리며, 위쪽 부분의 받쳐주는 호도 역시 사이클로이드 모양이다. 이러한 호를 따라가는 진자는 진폭에 관계없이 주기가 정확히 일정하기 때문에 좀 더 정확한 진자시계를 만들 수 있다.

5 좀 더 정확한 운동의 기술

위에서 설명하고 유도한 식들은 진폭이 작을 때에 한하여 유효한 공식이다. 실제로는 각변위에 따른 [math] \theta [/math]의 변화가 선형이 아닌데, 이를 고려한 더 정밀한 근사 방법이 있다.

5.1 비선형 근사

비록 단순조화운동과 다른 양상을 보이지만 주기 운동이라는 점은 변하지 않는다. 전개되는 식은 여러 가지가 있으나 여기서는 가장 간단한 경우로 두 조화함수의 합으로 나타난다고 가정한다.

[math] \displaystyle \theta = A\sin\omega t + B\sin 3\omega t [/math]

그리고 위 사인 급수의 두 번째 항까지 남겨놓는다.(이 세제곱 항 때문에 위 시험해에서 각진동수를 [math] \omega [/math]와 [math] 3\omega [/math]로 둔 것이다.)

[math] \displaystyle \sin\theta \approx \theta -\frac{\theta^{3}}{6} [/math]

그러면 운동방정식은 아래와 같이 세워진다.

[math] \displaystyle \frac{d^{2}\theta}{dt^{2}}+\omega_{0}^{2} \theta- \frac{\omega_{0}^{2}}{6}\theta^{3}=0, \quad \omega_{0}= \sqrt{g \over \ell}[/math]

여기서 시험 해를 대입하여 가장 지배적인 항 두 개를 골라낸다.

[math] \displaystyle 0= A\left(-\omega^{2} + \omega_{0}^{2}-\frac{A^{2}}{8}\omega_{0}^{2} \right)\sin\omega t + \left(-9B\omega^{2} +B\omega_{0}^{2} - \frac{A^{3}}{24}\omega_{0}^{2}\right) \sin 3\omega t + \omicron [/math]

가장 오른쪽 항 [math] \omicron [/math] 은 [math] \omega [/math] 나 [math] 3\omega [/math] 이외의 진동수로 진동하는 작은 항들로, 편의상 무시한다. 두 번째 항에서 알 수 있듯이 작은 진동에서 [math] B [/math] 는 [math] A [/math] 보다 크기가 훨씬 작다. 즉 [math] A [/math] 를 진폭으로 둘 수 있다. 그리고 진동수가 [math] A [/math] 의 함수가 되므로 진폭에 따라 진자의 주기가 달라지게 됨을 알 수 있다.

[math] \displaystyle -\omega^{2} + \omega_{0}^{2}-\frac{A^{2}}{8}\omega_{0}^{2}=0 [/math]

[math] \displaystyle \omega = \omega_{0} \sqrt{1-\frac{A^{2}}{8}}, \quad \omega_0 =\sqrt{g \over \ell} [/math]

주기는 다음과 같이 근사적으로 계산된다.

[math] \displaystyle T \approx T_{0} \left(1-\frac{A^{2}}{8}\right)^{- {1 \over 2}} \approx T_{0} \left(1+\frac{\theta_{0}^{2}}{16}\right), \quad T_0 =2\pi\sqrt{\ell \over g} [/math]

즉, 진폭이 커질수록 주기는 길어진다.

5.2 정확한 풀이

이 위에 소개된 근사조차도 여전히 진폭이 너무 크지 않을 때에 한하여 유효하다. 가령 실이 아니라 단단한 막대로 연결되어 90도보다 큰 진폭이 허용되면, 이러한 근사 방식은 통하지 않는다. 더 정확한 운동방정식의 풀이를 위해서는 타원적분을 도입해야 한다. 위의 역학적 에너지 보존 식에서 아래 식을 얻었다.

[math]\displaystyle \frac{1}{2} \left(\frac{d\theta}{dt}\right)^{2}=\omega_{0}^{2}(\cos\theta-\cos\theta_{0}) [/math]

각도가 증가하는 경우

[math]\displaystyle \frac{d\theta}{dt}=2\omega_{0}\left(\sin^{2} \frac{\theta_{0}}{2} - \sin^{2}\frac{\theta}{2} \right)^{1 \over 2} [/math] (코사인의 2배각 공식 적용)

즉 진자가 [math] \theta = 0 [/math] 에서 시작하여 진폭 지점까지 올라가는 데 걸리는 시간(주기의 4분의 1)은 아래 식과 같이 주어진다.

[math]\displaystyle \omega_{0} t=\frac{1}{2}\int^{\theta}_{0}\left(\sin^{2} \frac{\theta_{0}}{2} - \sin^{2}\frac{\theta '}{2} \right)^{-{1 \over 2}} d\theta ' [/math]

[math]\displaystyle \omega_{0}\cdot \frac{T}{4}= \frac{1}{2} \int^{\theta_0}_{0}\left(\sin^{2} \frac{\theta_{0}}{2} - \sin^{2}\frac{\theta '}{2} \right)^{-{1 \over 2}} d\theta ' [/math]

여기서 다음과 같은 [math] \phi [/math] 를 도입하여 적분변수를 바꾸어 주면 제1종 타원적분을 얻을 수 있다.

[math]\displaystyle \sin\frac{\theta}{2}=k \sin\phi, \quad k=\sin\frac{\theta_{0}}{2}, \quad 0\lt\phi\lt\frac{\pi}{2} [/math]

이제 위의 적분방정식은 아래와 같이 변형된다.

[math]\displaystyle \omega_{0} t = \int^{\phi}_{0}\left( 1 - k^{2}\sin^{2} \phi ' \right)^{- {1 \over 2}} d\phi ' = F(\phi, k) = F(\sin\phi; k) [/math] (여기에서 [math] F [/math]는 제 1종 불완전 타원적분이다.)

[math]\displaystyle \omega_{0}\cdot \frac{T}{4} = \int^{\pi \over 2}_{0}\left( 1 - k^{2}\sin^{2} \phi ' \right)^{- {1 \over 2}} d\phi ' = F \left(\frac{\pi}{2}, k \right) = K(k) [/math] (여기에서 [math] K [/math]는 제 1종 완전 타원적분이다.)

따라서, 주기는 다음과 같이 표현할 수 있다.

[math]\displaystyle T=T_{0} \frac{2}{\pi} K(\sin\frac{\theta_{0}}{2}), \quad T_{0}=2\pi\sqrt{\ell \over g} [/math]

참고로 제 1종 완전 타원적분은 아래와 같이 무한급수로 펼칠 수 있다. 계산 사이트 링크

[math]\displaystyle \frac{2}{\pi} K(k) = 1+ \sum^{\infty}_{n=1} \left[k^{2n} \left(\Pi^{n}_{i=1}\frac{2i-1}{2i}\right)^{2}\right] [/math]

한편 위의 제 1종 불완전 타원적분 식의 역함수는 야코비 사인함수로 표현된다. 이는 각변위가 증가하는 경우 외에도 모든 [math] t [/math] 에서 성립한다. 웰컴 투 케이오스!

[math] \displaystyle \sin\frac{\theta}{2} = k \sin \phi = k \cdot \text{sn} (\omega_{0} t; k), k= \sin\frac{\theta_{0}}{2} [/math]

[math] \displaystyle \theta= 2\sin^{-1} \left(k \cdot \text{sn} (\omega_{0} t; k) \right)[/math]

만일 진폭이 180도에 한없이 가까워지면(즉 [math] k [/math] 값이 1에 한없이 가까워지면) 주기는 무한히 커진다.

[math] \displaystyle \theta= 2\sin^{-1} \left(\tanh (\omega_{0} t) \right) (k=1)[/math]

5.3 연직면 상의 원운동

역학적 에너지보다 좀 더 커져서 최고점(180도)에 이르고도 속력이 존재하여 원운동을 할 수 있다. 즉 연직면 상의 원운동이 된다.

이미지 출처
위 그림은 단진자에 관한 상그림을 나타낸 것이다. 가운데의 닫힌 곡선(원)은 진폭이 작을 때의 운동을 나타내며, 외곽에 있는 물결 모양곡선이 비주기 운동을 나타낸다.

단진자 운동의 예시
역학적 에너지가 한없이 커지면, 단진자의 운동은 등속 원운동에 한없이 가까워진다.

이 때 운동방정식은 아래와 같이 비슷한 모양으로 세워진다.
[math] \displaystyle \frac{1}{2} \left(\frac{d\theta}{dt}\right)^{2}=\omega_{0}^{2}(\cos\theta+2k^2-1), \quad k\gt1 [/math]

k를 저렇게 잡은 것은 모양을 간단하게 하기 위함이다. 각도가 증가하는 경우

[math]\displaystyle \frac{d\theta}{dt}=2\omega_{0}\left(k^2 - \sin^{2}\frac{\theta}{2} \right)^{1 \over 2} [/math]

마찬가지로 타원 적분을 도입할 수 있다. 여기서 [math]\quad \phi = 2\theta[/math]
[math]\displaystyle k \omega_{0} t=\int^{\theta}_{0}\left(1 - k^{-2} \sin^{2} \phi ' \right)^{-{1 \over 2}} d\phi ' = F(\sin\phi; k^{-1})[/math]

여기서 T'은 연직면상의 원운동의 주기로, 위의 '왕복 주기'와 다른 값이다. 주기의 4분의 1이 지나면
[math]\displaystyle k \omega_{0}\cdot \frac{T'}{4}= \int^{ \frac{\pi}{2} }_{0}\left(1 - k^{-2} \sin^{2} \phi ' \right)^{-{1 \over 2}} d\phi ' = K(k^{-1})[/math]

결과는 아래와 같다. k의 값은 주어진 조건에 따라 결정되는 값으로, 역학적 에너지로부터 알아낼 수 있다.
[math] \displaystyle \sin\frac{\theta}{2} = \sin \phi = \text{sn} (k \omega_{0} t; k^{-1}), \theta = 2\sin^{-1} \left(\text{sn} (k \omega_{0} t; k^{-1}) \right)[/math]

[math] \displaystyle T' = T_0 \frac{2}{k\pi} K(k^{-1}) [/math]