외심

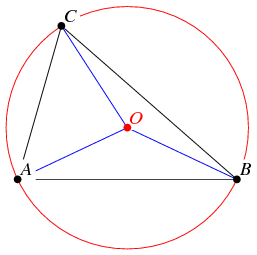
[math]\triangle{ABC}[/math]의 외심 [math]O[/math]

1 개요

한자 : 外心
영어 : Circumcenter

O원이 어느 삼각형의 세 꼭짓점을 모두 지닐때 원이 삼각형에 외접한다고 하며 O 원이 어느 삼각형의 외접원이라고 하고. O 원의 중심을 외심이라고 한다.

외심은 삼각형마다 위치하고 있는곳이 다른데, 예각삼각형은 삼각형 내부에, 둔각삼각형은 삼각형 외부에, 직각삼각형은 삼각형의 빗변의 중점에 위치하게 되고. 정삼각형은 삼각형의 중심이 외심이된다.

정삼각형은 방심을 제외한 삼각형의 오심이 모두 같다.

2 찾는 법

삼각형의 세 변의 수직 이등분선을 모두 그으면 만나는 한 점이 있는데, 그 점이 바로 삼각형의 외심이다.

찾는게 어렵다면 위에서 말한 삼각형의 종류에 따른 외심의 위치를 참고해보면 좋다.

3 성질

1. 외심에서 삼각형의 세 꼭짓점으로 이어지는 선분의 길이는 모두 같으며, 이 선분은 외접원의 반지름이 된다.
2. 삼각형의 수직 이등분선을 이어서 만나는 점이 외심이 된다.
3. 사인 법칙

[math]\overline{AB}=c, \overline{BC}=a, \overline{CA}=b[/math], 외접원의 반지름을 [math]R[/math]이라고 할 때,

[math]\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R[/math]

1. 외심에서 두 꼭짓점을 이어 만든 두 각은 나머지 각의 두 배이다.

4 기타

삼각형의 외심, 무게중심, 수심은 항상 일직선 위에 있다.