IS-LM 모형


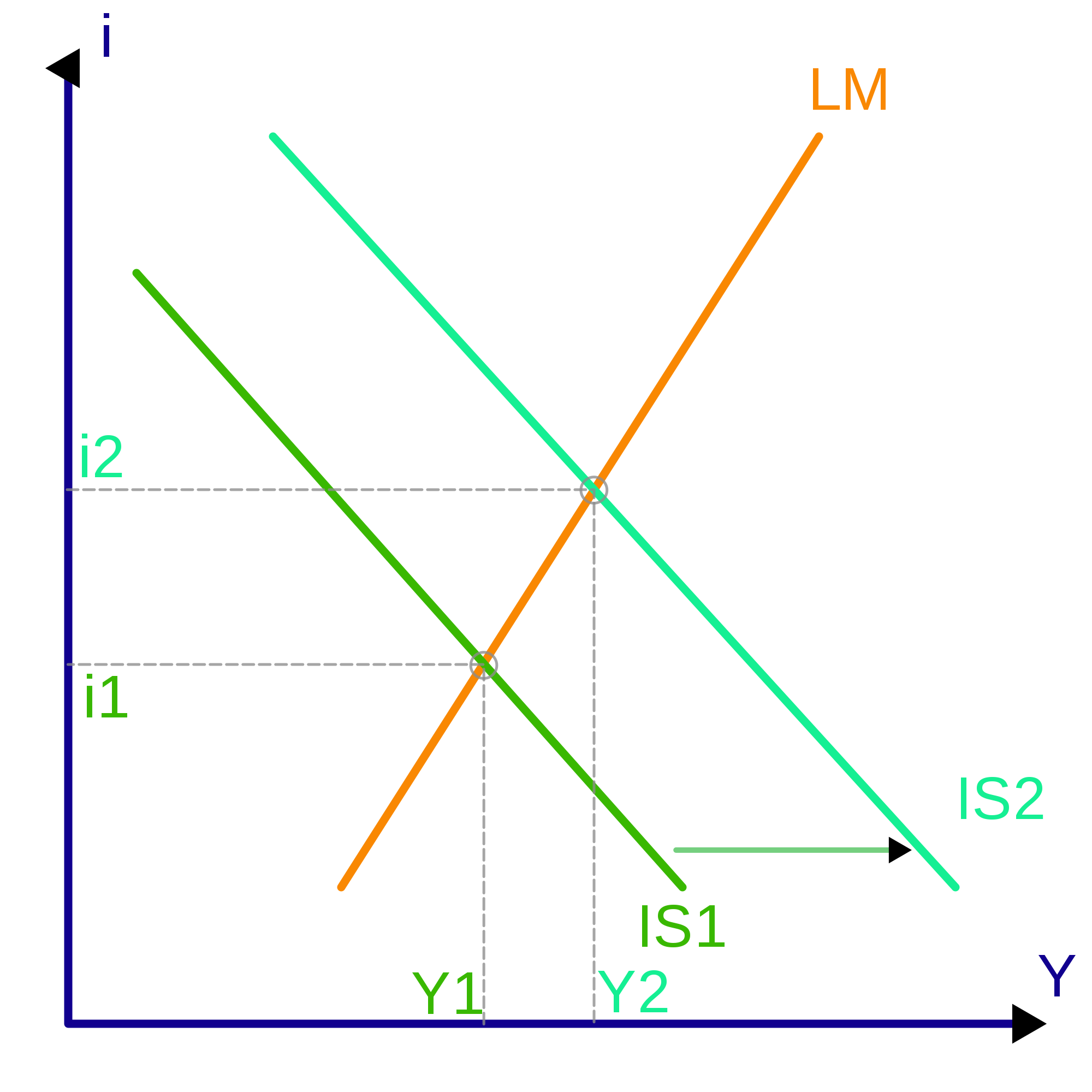
IS-LM모형 상에서 IS곡선이 우측이동하여 이자율과 국민소득이 상승하는 상황을 나타낸 그림.

1 개요

학부생들이 거시경제학에서 자주 배우는 경제모형.

케인지안의 논리를 수학적으로 표현한 모델로, 존 힉스가 1937년에 개발했다.[1] 실물시장과 화폐시장을 연결하는 이론으로, IS 곡선(Investment-Savings)과 LM 곡선(Liquidity preference-Money supply)의 교차점에서 산출량 Y와 이자율 r가 결정된다는 내용을 담고 있다.

명목 이자율인 i와 실질 이자율인 r은 피셔 방정식에 따라 인플레이션 기대에 좌우된다. 그러나 인플레이션 기대가 0이라는 가정 하에 i=r로 가정하여 IS-LM 곡선에서 명목 이자율을 구할 수 있다. 위 그래프는 인플레이션 기대가 0이라는 가정 하에 실질 이자율 r 대신 명목 이자율 i을 변수로 삼고 있다.

IS곡선은 주어진 이자율에 실물시장이 어떻게 반응하는가를 담은 곡선이다. 이자율이 높을수록 투자의 기회는 적어지고, 그만큼 실물경제의 산출량은 줄어들 것이다. 이 두 변수의 변화를 중심으로 하여 실물시장이 취할 수 있는 균형값들을 모은 것이다.
LM 곡선은 주어진 이자율에 금융시장이 어떻게 반응하는가를 담는다. LM곡선은 화폐시장의 균형점들을 모은 곡선이다. 이 균형점을 결정할 때의 논리는 다음과 같다. 화폐에 대한 수요는 경제의 산출량과 이자율에 달려있으며, 화폐의 공급은 중앙은행에서 정한다. 이 때 화폐의 수요와 공급이 만나는 점에서 이자율이 결정된다.

최근 학계에서 IS-LM 모형은 자주 쓰이지 않는 추세이다. 가장 큰 문제점은 여러 변수들과 변수 사이의 관계를 단순히 주어진 것으로 받아들인다는 것인데, 이는 합리적 기대에 위반되기 때문이다.[2] 그러나 가르치기 용이하다는 점과 기본적인 직관을 보여준다는 점에서 그리고 계속 가르쳐왔었기 때문에 학부에서는 아직 많이 가르치고는 한다. 폴 크루그먼같은 경우, 학부 수준에서는 IS-LM과 같은 임시변통적(ad-hoc) 모형을 배우는 것에도 중요한 가치가 있다는 주장을 했다.#

학계를 벗어난 월가나 중앙은행 등에서는 아직도 IS-LM모형을 주요하게 참고하는 경우가 있다. 이유는 여러가지가 있으나 몇가지를 들자면 다음과 같이 정리해볼 수 있다.

  • 대부분이 IS-LM을 배웠기 때문에, 모두가 이해할 수 있다.
  • 첫번째 근사값(first order approximation)으로서 충분히 역할을 한다. 모든 모형은 현실을 축약해서 설명한다는 점에서 일정 부분 잘못되어 있다. 그러므로 모형의 평가기준에서는 모형이 맞는지보다는 실제 정책결정 및 예측에서 제 역할을 하는지가 중요한 요건이다. 즉 모형의 가정에는 무엇이 있으며 또 그 가정이 어느 정도 위반되었을 때에도 얼마나 모형이 현실을 설명할 수 있는가에 있다. IS-LM의 경우 애초에 거시경제에 대한 단기예측을 위한 모형이며, 또한 단기적으로 무난하게 들어맞고, 많은 정책적 요인을 설명할 수 있으므로 좋은 모형이다.

2 확장

AD-AS 모형의 일부로서 쓰이기도 하며, LM 곡선 대신 화폐정책곡선(MP곡선)을 사용한 IS-MP 모형도 있다. 또한 해외 시장을 포함하여 균형을 구하는 IS-LM-BP 모형도 존재한다.

IS-MP 모형은 IS-LM 모형의 LM 곡선을 MP(Monetary Policy)곡선으로 대체한 모형이다. 이 모형은 데이비드 로머가 2000년에 주장한 것으로[3], 로머에 의하면 현대에 와서는 중앙은행이 더 이상 화폐공급량 그 자체를 타게팅하지 않으며 테일러 규칙등에 의해 조절하므로 이를 반영해야 한다는 것이다. 로머는 학부생들을 위하여 거시경제학 교과서의 IS-LM을 IS-MP로 대체한 학습자료를 2006년에 작성하였다.[4] #(영문)

그레고리 맨큐는 자신의 블로그 포스팅에서 IS-LM과 IS-MP 사이에는 실증적 혹은 이론적 차이가 거의 존재하지 않으며 단지 현학적인(pedagogal) 차이가 있을 뿐이라고 주장하였다.

IS-LM-BP 모형은 기존의 IS-LM모형에 BP(Balance of Payment), 즉 국제수지를 포함한 모형이다. BP곡선은 완전한 자본의 이동을 가정할 경우 수평으로 표시되며[5], IS, LM, 그리고 BP의 세 곡선이 만나는 점에서 균형이 이루어진다. 자세한 설명은 먼델-플레밍 모형을 참고할 것.
  1. ↑ 이후 1953년 Hansen에 의해 내용이 추가되어, Hicks-Hansen 모형이라고 부르기도 한다.
  2. ↑ 예를 들어 크리스토퍼 심스 교수의 입장(Wither ISLM) 등.
  3. ↑ Romer, David (2000). "Keynesian Macroeconomics without the LM Curve".
  4. ↑ 맨큐가 쓴 '거시경제학' 교과서 제 5판과 같이 쓰도록 작성했다고 한다.
  5. ↑ Y가 x축, r이 y축이 되도록(즉 보통의 경제학 교과서처럼) 그릴 경우에 그렇다.