이항계수를 구하는 방법에 대해서는 파스칼의 삼각형 문서를 참조하십시오.
Pascal's Law
1 개요
1653년에 블레즈 파스칼이 발견한 원리. 밀폐된 용기에 담긴 비압축성 유체[1]에 가해진 압력은 유체의 모든 지점에 같은 크기로 ”전달”된다는 원리다. 또한 유체의 압력은 어느 방향에서나 동일하게 나타낸다. 이는 유압 장치의 원리로, 마치 도르래처럼 작은 힘으로 무거운 물체를 들어올릴 수 있게 해준다.
1.1 상세
위에서 압력이 유체에 동일하게 전달된다는 표현에 가끔 혼동하는 사람도 있는데, 유체의 모든 지점에서 압력의 크기가 같다는 원리가 아니다.
파일:파스칼의 원리.png
유체의 한 지점에서 나타나는 압력 자체는 일반적으로 아래가 위보다 크다. 바다의 수압이 아래로 갈수록 커지는 관계를 생각하면 된다.
파스칼의 원리에서 이야기하고자 하는 점은 위 그림에서 [math]\Delta P[/math] 값이 위치에 관계없이 일정하다는 것이다. 이때 [math]\Delta P=P'-P[/math]는 외부에 힘이 가해졌을 때 더해지는 압력이다.
더 엄밀히 말하자면, 외력이 없을 때 유체의 표면으로부터 깊이가 같은 모든 지점에서의 압력의 크기가 같다. 외력이 있을 경우 압력의 변화 [math]\nabla P[/math] 가 외력에 비례하여 생겨난다. 참고로 위 그림상에서는 [math]\rho g[/math]가 중력에 의해 생겨난 [math]\nabla P[/math]에 대응된다.
2 유압장치
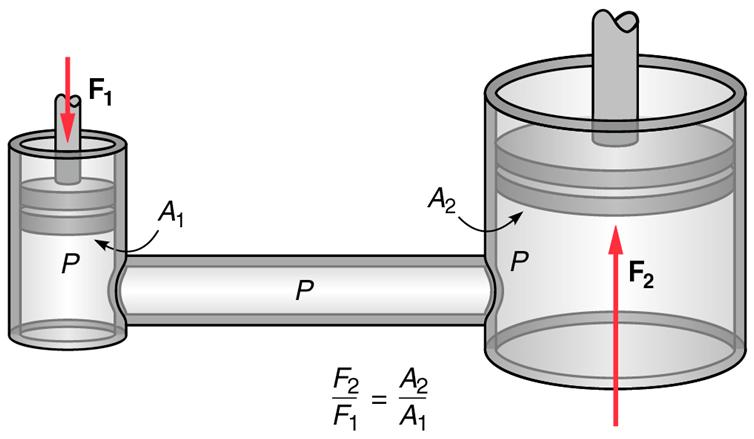
위 그림에서 단면적이 [math] A_1 [/math]인 피스톤에 가해진 압력 [math] F_1 [/math]가 전달되면 단면적이 [math] A_2 [/math]인 피스톤에 [math] F_2 [/math]만큼 전달된다.
한편, 피스톤 안의 유체는 비압축성이므로 단면적 [math] A_1 [/math]인 피스톤에 의해 밀려난 유체의 부피는 단면적 [math] A_2 [/math]인 피스톤에 채워진 유체의 양과 같게 된다. 이를 [math] V[/math]라고 하고 단면적[math] A_1 [/math] 피스톤이 내려간 거리를 [math] d_1 [/math], 단면적 [math] A_2 [/math] 피스톤이 올라간 거리를 [math] d_2 [/math]라고 하면 [math] V=A_1 d_1=A_2 d_2 [/math]이다. 또한 (도르래와 마찬가지로) 일의 원리에 의해 양 피스톤이 한(받은) 일의 양 [math]W [/math]은 같으므로 [math] W=F_1 d_1 = F_2 d_2 [/math]이다.
이렇게 부피와 일에 대해 나온 두 식을 정리하면, [math]\displaystyle \frac{F_1}{A_1} [/math](가해지는 압력 [math] P_1 [/math])=[math]\displaystyle \frac{F_2}{A_2} [/math](가해지는 압력 [math] P_2 [/math])라는 공식을 얻을 수 있다.
| 기준 | 유압장치 | 지레[2] |
| 힘(F) | (입력 힘)<(출력 힘) | |
| 변위(d) | (입력 변위)>(출력 변위) | |
| 입력/출력 부분에서 같은 값 | 압력(P=F/A) | 돌림힘(τ=F·L) |
| 변인 | 피스톤의 면적(A) | 받침대에서 떨어진 거리의 역수(L-1)[3] |
3 예시

- 자동차의 유압 브레이크: 브레이크 페달을 밟아 압력이 높아지면 브레이크액을 통해 동일한 힘이 4개의 바퀴에 고르게 전달되면서 모든 바퀴에 균등하게 제동력을 전달할 수 있다. 이때 비압축성 유체의 역할을 하는 브레이크액의 관리가 상당히 중요한데, 위에서 설명했듯이 파스칼의 원리는 비압축성 유체에 대해 적용되는 것인데, 브레이크액에 기포가 차버리면 압축이나 팽창이 되므로 압력이 제대로 전달되지 않아 브레이크가 제대로 듣지 않는 매우 위험한 일이 발생할 수 있기 때문이다. 베이퍼 록 현상 문서를 참고.

- 유압식 리프트: 공기 압축기를 통해 기름통의 기름에 압력을 가하면 이 압력이 실린더의 기름에 전달되어 자동차를 들어올릴 수 있다. 도면에서는 힘을 키우는 방향이 일반적으로 생각하는 것[4]과 다르며, 자동차가 있는 쪽에 가해지는 힘은 공기 압축기가 내는 힘보다 작지만 이동 거리가 더 크다. 공기압축기의 출력은 남아도는데 자동차를 매우 정밀하게 움직여야 하는 상황인가 보다.
그냥 잘못 그렸겠지

- 치약: 일부 치약은 두 가지 색이 십자 형태로 나오는데, 용기 내부에는 각각의 색이 십자 형태로 충전되어 있고 용기를 누르는 힘이 전체에 고르게 퍼져 형태가 뭉개지지 않고 나온다.
어렸을 때 이거 궁금했을 사람 있을 거다.

- 로봇팔, 톨게이트 요금 낼 때 요긴한 그 것.

도면에 에러가 있는데, 몸 전체에 일정한 힘이 가해지는 것이 아니라 일정한 압력이 가해지는 것이다. 물론 저 도면이 일반인 대상이라는 점을 감안할 때, 적확한 물리학 용어를 사용하지 않았다고 비판하기에는 무리가 따른다.