
1 개요
Eratosthenes. 고대 그리스의 수학자이자 지리, 천문학자. 생몰년도는 기원전 273?~192?
호기심이 많아서 동시에 여러 학문을 공부했고, 손을 댄 학문들의 거의 다가 최고는 아니더라도 두 번째의 실력을 가졌기 때문에 여러 분야를 공부하다 보니 딱히 1등인 분야가 없어서 '언제나 2등' 이라는 뜻의 'β(베타)'라는 별명으로 다른 학자들에게 불려졌다. 콩라인
칼 세이건의 코스모스에서 언급한 바에 따르면, 당대의 대도시 알렉산드리아에 있는, 알렉산드리아 도서관의 관장이었다고 한다. 지동설을 최초로 주장했던 아리스타르코스의 친구이기도 했다.
잘 알려지지는 않았지만, 당대의 그는 문학가로써의 이름이 더 드높았다고 한다.[1]
2 일화
2.1 지구의 둘레
하짓날 시에나와 알렉산드리아의 태양 그림자가 다르다는 것을 발견, 이를 응용하여 지구의 둘레를 세계 최초로 계산한 적이 있다.
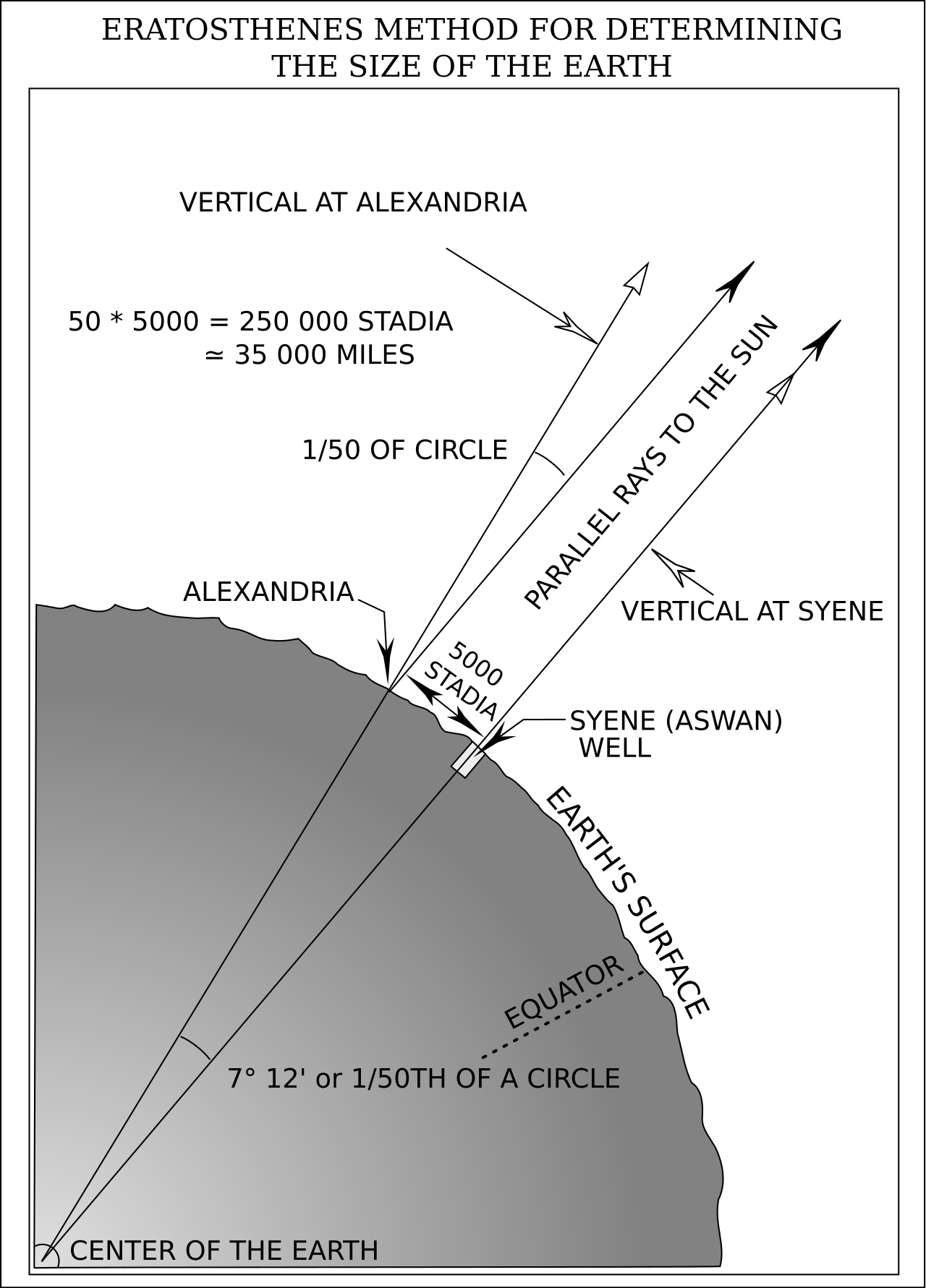
시에나-알렉산드리아 간 거리가 대략 5000스타디아(약 925km)이며 위도 차이가 7.2도라는 점을 이용하여 지구 둘레가 250000스타디아(46250km)라고 계산하였다. 실제 지구의 둘레는 약 4만 km이며 이러한 오차는 시에나와 알렉산드리아가 같은 경도에 위치하지 않으며, 두 장소 간 거리에 내재된 오차가 증폭되어 발생한 것이다. 하지만, 고대 그리스 시대라는 당시의 과학 기술을 생각한다면[2] 상당히 정확한 계산이라고 보는게 타당할 것이다.
2.2 지축의 기울기 계산
지구의 자전 축은 공전궤도에 대해 조금 기울어져 있다. 에라스토테네스는 이 기울기 또한 계산해 냈다. 역시 놀랄만큼 정확하게.
2.3 에라토스테네스의 체
에라토스테네스가 고안해낸 소수를 찾아내는 방법. 체를 쳐내듯이 합성수를 하나하나 지워나가며 소수만을 골라내는 방법이다. 자세한 건 본 문서 참조.
현재까지 소수를 구할 때 쓰는 방법들은 많이 나왔으나, 유한히 주어진 구간 내에 있는 모든 소수를 찾을 수 있는 가장 빠르고도 확실한 방법은 이 방법밖에 없다.