| 정다면체 | ||||
| 플라톤 다면체 볼록 정다면체 | 케플러-푸앵소 다면체 오목 정다면체 | |||
| 정사면체 | 정육면체, 정팔면체 | 정십이면체, 정이십면체 | 작은 별모양 십이면체, 큰 십이면체 | 큰 별모양 십이면체, 큰 이십면체 |
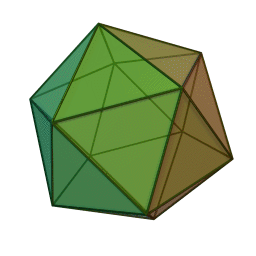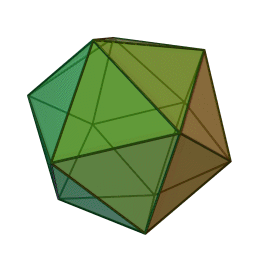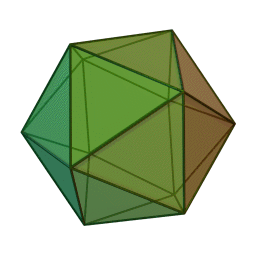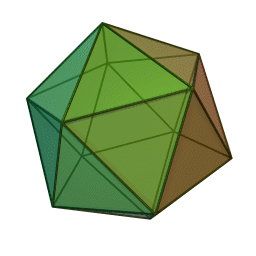
정다면체중 하나인 정이십면체의 모습.
1 개요
正二十面體, Icosahedron[1]
한 개의 꼭짓점에 다섯 개의 정삼각형이 만나고, 총 스무 개의 면으로 이루어진 다면체. 정다면체들 중 가장 많은 수의 면을 가졌다.
정이십면체에서 두 면이 이루는 이면각은 [math]\displaystyle\sin^{-1}\frac{-\sqrt{5}}{3}\approx138.19^\circ[/math]로, 3개의 정이십면체가 한 모서리에서 만난다고 가정하면 414.57º로 360º를 초과하기 때문에 4차원 볼록 정다포체를 만들 수 없다.[2]
2 정이십면체에 대한 정보
| 단위/특성 | 개수 | 비고 |
| 슐레플리 부호 | {3,5} | |
| 꼭지점(vertex, 0차원) | 12 | |
| 모서리(edge), 1차원) | 30 | |
| 면(face, 2차원) | 20 | 정삼각형 |
| 쌍대 | 정십이면체 {5,3} | |
| 포함 관계 또는 다른 이름 | 비틀어 늘린 맞붙인 오각뿔 (Gyroelongated bipyramid)[3] 다듬은 사사면체 (Snub Tetratetrahedron)[4][5] 다듬은 정팔면체 (Snub octahedron) 다듬은 엇정삼각기둥 (Snub triangular antiprism)[6] |
한 변의 길이가 [math]a[/math]인 정이십면체가 있을 때
외접구의 반지름 =[math]\displaystyle\frac{\sqrt{10+2\sqrt{5}}}{4}a[/math][7]
내접구의 반지름 = [math]\displaystyle\frac{\sqrt{3}}{12}(3+\sqrt{5})a[/math]
총 모서리 길이(total edge length) = [math]30a[/math]
겉넓이(surface area) = [math]5\sqrt{3}a^2[/math]
부피(volume) = [math]\displaystyle\frac{5}{12}({3+\sqrt{5}})a^3=\frac{5\varphi^2}{6}a^3[/math]
2.1 다른 정다면체들과의 관계
3 현실에서의 예시
- ↑ 복수는 Icosahedra
- ↑ 정이십면체로 오목 정다포체는 만들 수 있다.
- ↑ 정이십면체는 정오각뿔, 엇정오각기둥 그리고 다시 정오각뿔을 정오각형 면끼리 순서대로 붙여 만들 수 있다.
- ↑ 아르키메데스 다면체의 다듬기 항목 참조. 정사면체의 각 면을 띄워 놓고 각 꼭지점에 5개의 삼각형을 끼워 서로 이어가면 만들어진다.
- ↑ 정팔면체의 다른 이름이 사사면체다. 이유는 항목 참조.
- ↑ 엇정삼각기둥도 정팔면체의 다른 이름이다.
- ↑ 여기에서 φ는 황금비이다. [math]\displaystyle(\varphi=\frac{1+\sqrt{5}}{2})[/math]
- ↑ 어떤 다면체의 꼭지점을 면으로, 면을 꼭지점으로 대체한 다면체를 쌍대 다면체라고 한다.
- ↑ 정이십면체는 한 꼭지점에 다섯 개의 정삼각형이 만나기 때문에 {3, 5} 한 꼭지점에서 정오각형이 세 개 만나는 도형인 정십이면체{5, 3}와 쌍대 도형이다.
- ↑ 정확히는 약간 길쭉한 모양이나, 매우 유사하게 생겼다.
- ↑ 고압 환경에서 존재하는 붕소의 동소체이다.
- ↑ 잘 모르겠다면 골프공에 있는 딤플(골프공 표면에 존재하는 홈)을 자세히 보자. 가끔 예외인 골프공도 있을 수 있으나, 대부분의 골프공의 경우, 대부분의 딤플들은 주변의 6개 딤플들로 둘러싸여 있고, 단 12개의 딤플만 5개의 다른 딤플들로 둘러싸여있는데, 이 12개의 딤플을 이으면 정이십면체가 된다.
- ↑ 골프공과 마찬가지로 반드시 정이십면체 기반으로 만들 필요는 없으나, 대부분의 지오데식 돔의 경우, 정다면체들 중에서는 정이십면체가 구와 가장 가깝기 때문에 정이십면체를 기반으로 만들어진다.