4차원 정다포체

차원
0	1	2	3	4	5
점	선(길이)	면(넓이)	입체(부피)	초입체(초부피)

4차원 볼록 정다포체
정오포체	정팔포체	정십육포체	정이십사포체	정백이십포체	정육백포체

1 개요

↑ 정오포체	↑ 정팔포체	↑ 정십육포체
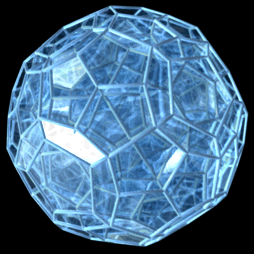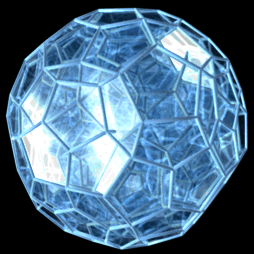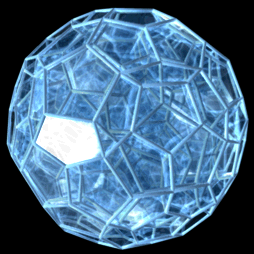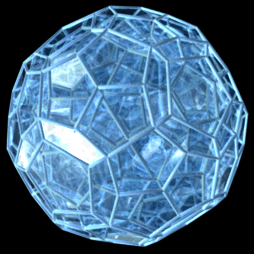↑ 정이십사포체	↑ 정백이십포체	↑ 정육백포체
회전하는 4차원 정다포체들을 3차원에 투영시킨 모습

四次元 正多胞體/4-Dimensional Regular Polychoron (또는 regular polychoron, regular 4-polytope)

기하학에 등장하는 4차원 도형의 일종.

4차원 다포체 중에서 모든 면이 합동인 정다면체로 이루어져 있으며, 각 선분에서 만나는 입체의 개수가 같은 다포체를 말한다.

2 종류

여섯 개의 볼록 정다포체와 열 개의 오목 정다포체가 존재한다.

2.1 볼록 정다포체

({p,q,r}은 슐레플리 부호.)

• 정오포체 : 5개의 정사면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 3개. : {3,3,3}
• 정팔포체 = 테서랙트 : 8개의 정육면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 3개. : {4,3,3}
• 정십육포체 : 16개의 정사면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 3개. : {3,3,4}
• 정이십사포체 : 24개의 정팔면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 4개. : {3,4,3}
• 정백이십포체 : 120개의 정십이면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 3개. : {5,3,3}
• 정육백포체 : 600개의 정사면체로 이루어져 있다. 한 모서리에서 만나는 입체의 개수는 5개. : {3,3,5}

2.2 오목 정다포체

• 큰 거대 별모양 백이십포체 (Great Grand Stellated 120-cell) : {5/2, 3, 3}
• 큰 별모양 백이십포체 (Great Stellated 120-cell) : {5/2, 3, 5}
• 거대 별모양 백이십포체 (Grand Stellated 120-cell) : {5/2, 5, 5/2}
• 작은 별모양 백이십포체 (Small Stellated 120-cell) : {5/2, 5, 3}
• 큰 이십면체 백이십포체 (Great Icosahedral 120-cell) : {3, 5/2, 5}
• 거대 육백포체 (Grand 600-cell) : {3, 3, 5/2}
• 정이십면체 백이십포체 (Icosahedral 120-cell) : {3, 5, 5/2}
• 큰 거대 백이십포체 (Great Grand 120-cell) : {5, 5/2, 3}
• 큰 백이십포체 (Great 120-cell) : {5, 5/2, 5}
• 거대 백이십포체 (Gand 120-cell) : {5, 3, 5/2}

2.3 입체와 면과 모서리와 꼭지점의 개수

볼록 정다포체의 입체의 개수를 [math]C[/math], 면의 개수를 [math]F[/math], 모서리의 개수를 [math]E[/math], 꼭지점의 개수를 [math]V[/math]라고 할 때,
[math]V-E+F-C[/math] [math]=[/math] [math]0[/math]이다.

정다포체	입체의 개수	면의 개수	모서리의 개수	꼭지점의 개수
정오포체	5	10	10	5
정팔포체	8	24	32	16
정십육포체	16	32	24	8
정이십사포체	24	96	96	24
정백이십포체	120	720	1200	600
정육백포체	600	1200	720	120

3 여담

플라톤이 5개의 볼록 정다면체에 그리스의 4원소들을 대응시켰듯, 정식명칭은 아니지만 4차원 정다포체에 대해서도 4원소설의 원소들과 대응되는 이름으로 부르는 사람들이 있다. 단, 4차원 볼록 정다포체는 총 6개로 4원소+(5번째 원소인 에테르)를 만족시키기 어려우므로 정이십사포체에 대하여 동양의 음양오행설에서의 나무를 따와 Xylochoron(xylo- : 나무)이라고 부른다.

원소	대응되는 플라톤의 정다면체	대응되는 정다포체 (별명)
불	정사면체	정오포체 (pyrochoron)
땅	정육면체	정팔포체 (geochoron)
공기	정팔면체	정십육포체 (aerochoron)
나무(4원소설의 원소가 아님)		정이십사포체 (xylochoron)
에테르(또는 공간, 또는 우주)	정십이면체	정백이십포체 (cosmochoron)
물	정이십면체	정육백포체 (hydrochoron)

단체(simplex), 초입방체(hypercube), 또는 정축체(orthoplex)가 아닌 볼록한 정다포체는 4차원 유클리도 공간까지만 존재한다. 즉, 5차원부터는 볼록한 정다포체가 오직 3개까지만 존재한다.

4 연관항목

• 4차원
• 정다면체