| 아르키메데스 다면체 Archimedean Solids | ||||
| 준정다면체 Quasiregular Polyhedra | 반정다면체 Semiregular Polyhedra | |||
| 육팔면체 십이이십면체 | 깎은 정사면체 깎은 정육면체, 깎은 정팔면체 깎은 정십이면체, 깎은 정이십면체 | 깎은 육팔면체 깎은 십이이십면체 | 마름모육팔면체 마름모십이이십면체 | 다듬은 육팔면체 다듬은 십이이십면체 |
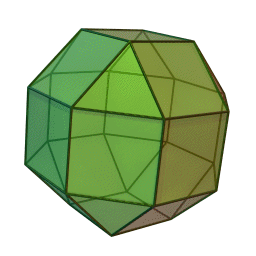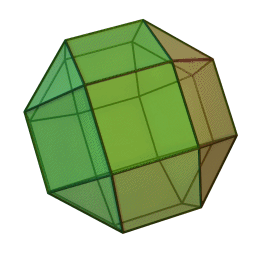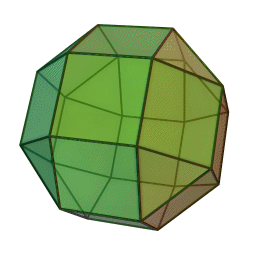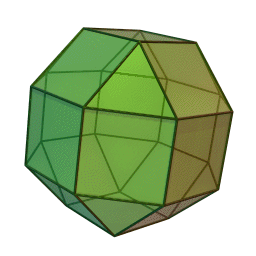
반정다면체 중 하나인 마름모육팔면체의 모습.
1 개요
마름모六八面體, Rhombicuboctahedron[1]

한 꼭지점에 정삼각형 한 개와 정사각형 세 개를 배치해 만든 반정다면체. 위 그림과 같이 정육면체의 각 모서리들을 정사각형으로, 각 꼭지점들을 정삼각형으로 대체하거나, 정팔면체의 각 모서리들과 꼭지점들을 정사각형으로 대체하여 만들 수 있다. 이 과정이 마치 다면체를 부풀리는 것 같다고 하여(expansion) 부풀린 정육면체/정팔면체/육팔면체라고도 불린다.
2 마름모육팔면체에 대한 정보
| 단위/특성 | 개수 | 비고 |
| 슐레플리 부호 | rr{3,4} 또는 rr{3,4}[2][3] t0,2{3,4} 또는 t0,2{4,3}[4] | |
| 꼭지점 형태 | 3.4.4.4[5] | |
| 꼭지점(vertex, 0차원) | 24 | |
| 모서리(edge), 1차원) | 48 | |
| 면(face, 2차원) | 26 | 정삼각형×8, 정사각형×18 |
| 쌍대 | 연꼴이십사면체 | |
| 포함 관계[6] 또는 다른 이름[7] | 늘린 맞붙인 두 사각지붕(Elongated square orthobicupola)[8] |
[9]
한 변의 길이가 [math]a[/math]인 마름모육팔면체가 있을 때
외접구의 반지름 = [math]\displaystyle\frac{\sqrt{5+2\sqrt{2}}}{2}a[/math]
겉넓이(surface area) = [math](18+2\sqrt3)a^2[/math]
부피(volume) = [math]\displaystyle\frac{2}{3}(2+5\sqrt{2})a^3[/math]
3 현실에서의 예시
- ↑ 복수는 rhombicuboctahedra
- ↑ r은 절반 지점까지 깎은 상태를 의미한다. rr{3,4}와 rr{4,3}은 정팔면체나 정육면체를 모서리 절반 지점까지 깎아 육팔면체를 만들고 다시 꼭지점을 깎아내어 마름모육팔면체형으로 만든다는 의미이다.
- ↑ 실제로는 아무리 육팔면체를 잘 깎아도 깎은 면이 정다각형으로 나오지 않는다. 육팔면체의 꼭지점 형태는 3.4.3.4로, 다각형들이 서로 같지 않기 때문에 단면이 정사각형이 아닌 인접한 두 변의 길이의 비가 1:√2인 직사각형이 나온다
- ↑ t0,2는 부풀리기(expansion)을 의미한다.
- ↑ 한 꼭지점에 정삼각형-정사각형-정사각형-정사각형 순서대로 모인다는 뜻. 나머지는 모두 같은 정사각형들이고, 정삼각형은 1개밖에 없으므로 다르게 배열해도 똑같다.
- ↑ 반드시 이 다면체를 지칭하지는 않으며, 해당 이름이 비슷하게 생긴 고르지 않은 다면체도 포함하는 경우
- ↑ 반드시 이 도형과 닮거나 합동인 도형을 지칭하는 이름
- ↑ 사각지붕(J7)은 마름모육팔면체를 정팔각형을 이루는 모서리들을 기준으로 잘랐을 때, 작은 조각과 같으며, 존슨 다면체이다.
- ↑ 슐레플리 부호로 [math]r\begin{Bmatrix}3\\4\end{Bmatrix}[/math]라고 쓰기도 한다.
- ↑ 가끔 석가탄신일 등 연등행사가 있는 날에 이런 형태의 연등을 볼 수 있다.