응력

• 상위 항목: 물리학 관련 정보, 기계공학, 재료공학

應力 yes power!!
Stress 구하려다 오히려 받는것
[math]\sigma[/math], [math]\tau[/math]

1 정의

외부에 힘을 받아 변형을 일으킨 물체의 내부에 발생하는 단위면적 당 힘. 고체역학 혹은 재료역학에서 재료의 변형을 다룰 때 변형율과 함께 등장한다. 똑같이 단위면적 당 힘인 압력과 단위는 같지만 의미는 전혀 다르다. 압력은 응력의 대각 성분의 평균으로 정의되는 스칼라량이다.

힘이기 때문에 벡터일 것 같지만, 이녀석은 텐서(Tensor)로 표시된다. 2차 텐서로 나타낼 수 있기 때문에 보통 3차원에서 어느 물체의 내부에 한 지점에서의 응력을 표시할 때에는 3x3 행렬을 이용하여 나타낸다.

이 행렬에서 행은 힘이 작용하는 면을, 열은 힘이 작용하는 방향을 나타낸다. 예컨대 [math]\tau_{yz}[/math]의 경우 [math]y[/math]축을 법선벡터로 하는 면에서 [math]z[/math]축 방향으로 작용하는 힘을 가리킨다. 상자의 뒷면을 [math]xz[/math](즉, [math]y=0[/math])평면, 밑면을 [math]xy[/math]평면(즉, [math]z=0[/math])이라고 했을 때 [math]\tau_{yz}[/math]는 '앞면([math]y=y_1[/math])에서 위로 미는 힘에 의한 전단응력(상자의 면에 손바닥을 대고 미는 것처럼)' 혹은 '뒷면에서 아래로 미는 힘에 의한 전단응력'이 된다. [math]\sigma_{yy}[/math]는 '앞면을 잡아당길 때의 응력' 혹은 '뒷면을 앞으로 누를 때의 응력'. [math]\tau[/math] 성분을 '전단 응력', [math]\sigma[/math]성분을 '압축 응력' 또는 '인장 응력'이라고 하며 해당 내용은 후술한다.

물체를 아주 작은 상자들로 쪼갰을 때, 상자면에서 작용하는 힘이 면의 어떤 점에서나 일정하다면 법선벡터의 부호가 반대인 상자의 반대 면에 작용하는 [math]\sigma[/math], [math]\tau[/math]성분은 크기가 같고 방향이 반대이다. 물체가 평형상태라면 이 때 모멘트(토크, 짝힘, 각힘, 뭐라 부르든)가 보존되어야 하므로, 이 행렬은 대칭행렬이 된다. 즉 [math]\tau_{xy} = \tau_{yz}[/math]. 그래서 이 때 행렬의 9가지 성분 중 독립적인 성분은 6가지이다.

이 때 이 행렬의 축 벡터(pivot vector)를 취하면 [math]x, y, z[/math] 세 축에서의 수직 방향 응력을 알 수 있다.

2 탄성 한계 내에서 변형율과 응력

2.1 인장/압축 응력

引張/壓縮 應力
Tensile/Compressive Stress

어떤 재료의 중심축에 수직방향으로 작용하는 힘에 의한 응력. 방향에 따라 압축 응력과 인장 응력이 있다. 재료의 표면의 법선 방향으로 작용하므로 법선 응력/수직 응력(Normal Stress)이라고도 한다.

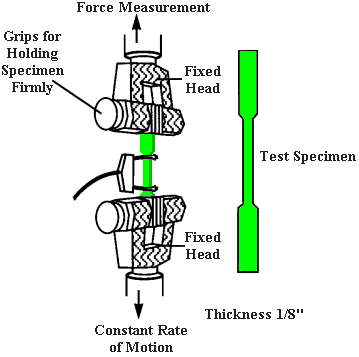
(재료의 인장 강도를 시험하는 대표적인 방식. 초록색으로 표시된 재료를 시간당 일정한 변형률에 따라 변형되도록 잡아당기고, 잡아당기는 데 드는 응력을 측정한다.)

길이가 [math]L[/math]인 어떤 기다란 재료 막대가 있다고 하자. 이 막대의 한 쪽 끝을 벽에 단단히 고정하고 다른 쪽 끝을 잡은 뒤 막대의 방향으로 크기 [math]F[/math]만큼의 인장력을 가하면 이 막대는 강체가 아닌 이상 길이가 늘어나는 변형이 일어난다. 이 때 재료 막대가 늘어난 길이를 [math]x[/math]라고 하자.

이 때 주어진 재료 막대의 변형율(Strain)은 [math]\epsilon[/math][math]=x/L[/math] 이다. 이 때 재료 막대의 변형은 다름아닌 응력에 의해 일어나는 것이다. 응력은 막대의 단면에 작용하는 단위면적당 힘이므로, 막대의 단면의 면적을 [math]A[/math]라고 했을 때 막대에 가해지는 응력은 [math]\sigma=F/A[/math] 이다.

재료 막대에 가하는 힘과 변형된 길이는 탄성 한계 내에서 비례한다는 것이 훅의 법칙(Hooke's Law)이므로, 재료 막대를 잡아당기는 힘 [math]F[/math]와 재료 막대가 늘어난 길이 [math]x[/math]의 관계는 다음과 같이 쓸 수 있다.

[math]F = kx[/math] (단, [math]k[/math]는 비례상수)

위 식의 양 변을 재료막대의 길이 [math]L[/math]과 재료 막대의 단면의 넓이 [math]A[/math]로 나눈다.

[math]F/LA = kx/LA[/math]

위 식을 정리하여 변형율과 응력에 대한 식으로 바꾸면 다음과 같다.

[math]\sigma = kL/A[/math]
　[math]= E\epsilon[/math]

여기에서 응력과 변형율이 탄성 한계 내에서 비례관계임을 알 수 있으며 비례상수 [math]kL/A[/math]는 [math]E[/math]로 바꾸어쓴다. 이 [math]E[/math]가 바로 탄성 계수(modulus of elasticity)이다. 탄성계수 [math]E[/math]는 물질의 고유한 성질이며, 여기에 재료의 단면적을 곱하고 재료의 길이로 나누면 그 재료의 스프링 상수를 알 수 있다. 일명 영의 계수(Young's modulus)라고 한다.

이 때 변형율 [math]\epsilon[/math]의 값이 양수일 경우 인장이라고 하며 이 때 작용하는 응력 [math]\sigma[/math]를 인장 응력(Tensile Stress)이라고 한다. 변형율의 값이 음수일 경우에는 압축이라고 하며 작용하는 응력을 압축 응력(Compressive Stress)이라고 한다.

2.2 전단 응력

剪斷 應力
Shear Stress

전단 응력은 어떤 재료의 면에 접하는 방향으로 작용하는 힘에 의한 응력이다. 때문에 접선 응력(Tangential Stress)로도 불린다. 이해가 안된다면 두꺼운 책을 놓고 책 표지에 손바닥을 댄 다음 옆으로 민다고 생각해보자. 이 때 책의 옆면은 직사각형에서 평행사변형 형태로 변형될 것이다. 이것이 바로 전단응력과 전단응력에 의한 변형이다. 또, 가위같은 것으로 물체를 자르는 것은 전단 응력에 의한 파괴를 이용한 것이다.

어떤 재료의 표면에 접선방향의 힘, 즉 전단력을 작용하였을 때 전단변형율(Shear Strain)은 재료가 기울어진 각도이다.

먼저 정육면체의 재료 블럭이 있다고 하자. 이 재료 블럭의 앞면은 정사각형 모양일 것이다. 그 뒤에 블럭의 윗면에 전단력을 가하면서 재료 블럭이 이동하지 않게 고정하면 블럭은 강체가 아닌 한 변형을 일으킨다. 이 때 앞면의 모양은 정사각형에서 평행사변형으로 변할 것이다. 이 때 앞면의 옆모서리가 밑면에 수직한 선(법선)에서 기울어진 정도가 바로 전단변형율 [math]\theta[/math]이다.

전단응력의 기호는 [math]\tau[/math]이고, 전단응력과 전단변형율의 관계는 다음과 같다.

[math] \tau = G\theta [/math]

여기서 [math]G[/math]는 전단계수(shear modulus) 혹은 강성계수(modulus of rigidity)이고, 탄성 계수와 마찬가지로 재료의 고유한 성질이다.

2.2.1 마찰력

마찰력은 전단력으로 작용한다. 전단력이 무엇인지 몰랐다가 위에서 전단력, 전단응력에 대한 설명을 읽은 독자는 블록이 기울어지게 한 면을 밀어내는 상황을 보면서 전단력은 전부 마찰력에 의해 발생한다고 생각할 수 있으나, 전단력은 다른 경우에 발생하기도 한다.

예를 들어, 이 항목의 맨 밑에서 볼 수 있듯이 전단력은 재료에 가해진 인장력 혹은 압축력이 내부에서 '비스듬한 법선력'과 '비스듬한 전단력'으로 분해되면서 발생하는 경우도 있다. 또한, 교량과 같은 보(Beam) 위에 하중이 놓여있을 때나 기둥의 중간에 중심축과 평행하지 않은, 횡방향 성분의 힘이 포함된 힘을 가할 때 전단력이 발생한다.(만약 종이를 높게 쌓은 경우에 가운데를 손가락으로 누르면 가운데가 튀어나온다. 이런 것도 전단력이 작용한 예)

2.3 비틀림 응력

torsion stress

위의 전단 응력 항목에서 재료 블럭의 밑면은 바닥에 단단히 고정되어 있었다. 그렇다면 이 재료 블럭을 물 위에 혹은 공기 중에 둥둥 띄워놓은 뒤 전단력을 가하면 어떻게 될까? 아마도 빙글빙글 돌 것이다. 만약 위에서 나온 정육면체 재료 블럭의 네 옆면의 위쪽에는 시계방향으로 전단력을 가하고 옆면의 아래 쪽에는 반시계방향으로 전단력을 가한다면 어떻게 될까? 위 쪽은 시계방향으로, 아래 쪽은 반시계방향으로 회전하려고 하면서 비틀릴 것이다.

즉, 비틀림은 전단 변형의 한 형태이다.

이번에는 원통형의 긴 재료 막대를 생각해보자. 이 막대의 밑면은 땅에 단단히 고정되어있다. 이 막대의 임의의 한 점 [math]A[/math]를 통과하는, 밑면에 수직한 선을 생각한 뒤, 이 선이 밑면과 닿는 점을 [math]O[/math]라고 하자. 그런 뒤 재료 막대를 비틀어 [math]\theta[/math]만큼 회전시켰다고 하자. 막대가 회전하게 되면 임의의 한 점 [math]A[/math]는 [math]A'[/math]으로 이동하게 된다. 그러면 선분 [math]\overline{OA}[/math]와 [math]\overline{OA'}[/math]의 각도가 바로 이 재료 막대의 전단 변형율이고, 이 전단 변형율을 γ라고 한다.

이 재료 막대의 단면의 반지름을 [math]r[/math]이라고 하고, 선분 [math]\overline{OA}[/math]의 길이를 [math]L[/math]이라고 하자. 만약 매우 심하게 막대를 비튼 경우라면 [math]\overline{OA}[/math]와 [math]\overline{OA'}[/math]의 크기는 다르겠지만, 우리가 가정하는 경우에서 전단 변형율이 3~3도를 넘어가는 경우는 거의 없으므로 [math]\overline{OA}[/math]와 [math]\overline{OA'}[/math]의 길이가 거의 같다고 할 수 있을 것이다. 따라서 전단 변형율 [math]\gamma[/math]와 비틀림 각 [math]\theta[/math] 사이에는 다음과 같은 관계가 성립한다.

[math]r\theta = L\gamma[/math]

그리고 [math]\gamma[/math]는 전단변형율이므로 비틀림에 의해 재료 막대 내부에 작용하는 전단 응력은 다음과 같다.

[math]\tau = G\gamma = G\theta(r/L) [/math]

그러므로 재료를 비틀 때 비틀림 각을 알고 재료의 비틀린 단면의 반지름과 재료의 길이, 전단 계수를 알면 재료 내부에 작용하는 전단 응력의 크기를 알 수 있다.

이 때 [math]G(r/L)[/math]을 비틀림 상수라고 한다.

2.4 푸아송 비와 인장력-전단응력 간의 관계

인장력이 작용하는 상황에서, 재료는 길이 방향으로 늘어나는 변형을 겪게 된다. 이 때 재료는 수직방향으로는 길이가 늘어나지만 수평방향으로는 길이가 줄어든다. 이것은 압축에서도 마찬가지인데, 이 때 횡방향으로는 길이가 오히려 늘어날 것이다. 이렇게 수직 방향으로 변형이 일어날 때 수평 방향으로도 변형이 일어난다.

이 때 수평 방향의 변형율을 수직 방향의 변형율로 나눈 것이 푸아송 비(Poisson's ratio)이다. 푸아송 비는 주로 [math]n[/math] 혹은 [math]\nu[/math]로 표기한다.

[math]\nu= - [/math] 횡방향 변형율 [math]/[/math] 종방향 변형율

앞에 음의 부호[math](-)[/math]가 붙는 이유는, 종방향 변형율이 양수일 경우 즉 인장일 경우 횡방향 변형율은 항상 음수이고, 횡방향 변형율이 음수일 경우 즉 압축일 경우 횡방향 변형율은 항상 양수임로 횡방향 변형율을 종방향 변형율로 나눈 값은 항상 음수이기 때문에 최종적인 값을 양수로 만들어주기 위한 것이다.

재료의 고유한 성질인 탄성 계수 [math]E[/math]와 전단 계수 [math]G[/math]는 푸아송 비를 통해 하나의 식으로 표현할 수 있는데, 그 식은 다음과 같다.

[math]G = E / 2(1+\nu)[/math]

즉, 전단 계수와 탄성 계수, 푸아송 비 중 두 개를 알 면 나머지 하나를 계산을 통해 구할 수 있는 것이다.

몇몇 폼 계열 재료처럼 미세 구조가 접혀진 고리 형태인 경우 인장력을 가했을 때 접혀진 고리가 펼쳐지면서 수평 방향의 길이가 늘어날 수 있다. 이렇게 인장과 압축시 수평 길이가 반대로 늘고 줄어드는 재료는 음의 푸아송 비(Negative Poisson's ratio)를 가진다고 말한다. 다만 덩어리로 된 통상 재료라면 포와송 비를 양수로 가정해도 크게 문제될 것이 없다.

3 응력-변형율 선도

파일:Attachment/응력/stress-strain.jpg
<출처 : 위키피디아 「응력-변형도 선도」(Stress-Strain Diagram)문서>

탄성 한계 내에서의 응력과 변형율의 관계는 위에 설명해놓았지만, 탄성 한계를 넘어간 영역에서의 응력과 변형율의 관계는 실험을 통해 알아내는 수밖에 없다.

위 선도는 재료 중에서 연성 재료의 응력-변형율 선도이다. (Stress-Strain Curve/Diagram)

위 선도에서 원점부터 2 까지 응력과 변형율이 비례관계를 가지는 구간을 탄성 구간(Elastic Region)이라고 한다. 이 구간 안에서는 탄성이 지배적으로 작용한다. 때문에 변형율이 탄성 구간 안에 있으면 재료는 탄성에 의해 원래 모습으로 돌아오게 된다.

위 선도에서 탄성 구간을 제외한 나머지 구간은 소성 구간 (Plastic Region)이라고 한다. 이 구간 안에서는 소성이 지배적으로 작용한다. 때문에 응력이 소성 구간까지 올라가면 재료는 다시 원래 모습으로 돌아올 수 없다.

그러나, 소성 구간에서 탄성이 작용하지 않는 것은 아니다. 재료의 변형율이 소성 구간의 중간 어느 지점까지 커지도록 한 후 재료에 힘을 가하는 것을 멈추면 재료는 그 변형된 그대로 가만히 있는 것이 아니라, 탄성에 의해 모습을 어느 정도 복원한다. 이를 탄성 복원(Spring back)이라고 한다.

만약 재료가 소성 구간에 있는 그래프 위의 임의의 점 P의 변형율까지 변형되었다가 응력이 사라질 경우, 재료는 점 P를 지나고 탄성 구간에서의 기울기와 똑같은 기울기를 가지는 직선이 가로축과 만나는 지점의 변형율로 되돌아간다. 그렇게 해서 점 P의 변형율보다는 적지만 값이 0은 아닌 변형율로 재료의 모양이 고정된다. 이 때 새롭게 고정된 재료의 변형율을 영구 변형(permanent deformation)이라고 한다.

위 선도를 보면 2에서 거의 수평으로 진행하는 구간이 있는데, 이 구간이 시작될 때의 응력을 항복 응력(Yield Stress) 혹은 항복 강도(Yield Strength)라고 하고 항복 구간이 시작되는 지점을 항복점이라고 한다. 이 응력에서는 응력이 변하지 않거나 조금만 변해도 변형율이 마구마구 늘어난다. 조금 두꺼운 쇠막대를 구부리다보면 어느 순간 확 굽어지는 경우가 있는데, 이때 바로 쇠막대에 가한 힘이 발생시긴 응력이 항복 응력을 넘어가서 그렇게 되는 것이다.

이 항복 응력 이후에 재료가 본격적으로 소성 구간으로 진입하고, 변형이 심해져 하중을 부담하는 능력이 떨어지거나 기계에서 이탈하는 경우가 생기기 때문에 보통 이 항복 응력보다 작은 적당한 응력을 허용 응력(Allowable Stress)으로 설정하곤 한다.

이는 실제 현장에서는 매우 중요하다. 실제 구조물이나 기계에서 부재에 작용하는 응력이 허용응력을 넘어설 경우 매우 위험할 수 있으며, 재료가 버틸 수 있는 최대한의 응력을 기준 강도라고 하고 연성 재료의 경우 항복점에서의 응력이 기준 강도이다. 이 때 기준 강도를 허용 응력으로 나눈 것이 안전율(Safety Factor)이다. 당연히 안전율이 높을 수록 좋다.

즉, 허용 응력 = 항복 응력 / 안전도. (A.Stress = Y.Stress / SF)

위 선도의 소성구간에서 가장 큰 응력이 나타나는 점을 극한 응력(Ultimate Tensile Stress) 혹은 극한 강도(Ultimate Tensile Strength)라고 한다.

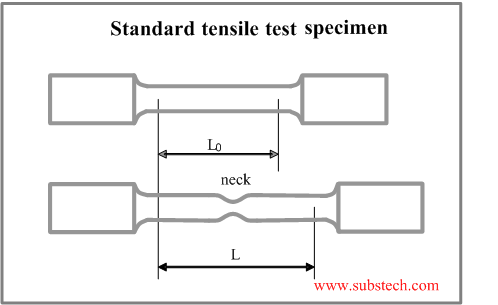
실험 도중에, 재료에는 극한 응력이 나타나기 조금 전부터 넥킹(Necking)이 일어난다. 가래떡의 예를 들어보면, 가래떡을 서서히 잡아당기면 가래떡 전체가 길게 늘어나다가 어느 순간 중간 부분이 다른 부분에 비해 잘록해진다. 이것이 바로 넥킹이다. 비록 실제 넥킹은 극한 강도가 나타나기 이전부터 나타나지만, 편의를 위해 극한 강도 이후의 구간을 '네킹 구간'이라고 부른다.

극한 응력 이후에는 응력의 크기가 작아지는데, 이는 실험의 한계로 인해 나타나는 것이다. 사실 넥킹이 일어나는 부위에서 응력-변형율의 관계는 일정하진 않아도 양(+)의 기울기를 가지는 관계이다. 하지만 이는 세로축의 물리량이 응력이기 때문에 나타나는 일이다. 넥킹이 일어나는 부위는 계속해서 잘록해지므로 힘이 그대로여도 넥킹에 의해 '힘/면적'인 응력의 크기는 계속 커진다. 하지만 우리가 실험을 통해서 응력을 측정할 때 대입하는 면적은 여전히 넥킹이 일어나지 않은 재료의 원래 단면적이다. 때문에 극한 강도 이후에 힘이 작어져도 변형이 계속되는 것이 마치 응력이 작아져도 변형이 계속되는 것으로 보이는 것이다. 실제로는 힘이 작아져도 면적이 작아지는 속도가 더 빨리 실제 응력은 계속 커지고 있다.

그래프가 어느 변형율에 이르면 끊어진다.
재료 자체가 파괴된 것이다.

3.1 재료의 종류에 따른 응력-변형율 선도

우리가 쓰는 고체 재료들은 대부분 연성 재료와 취성 재료로 나눌 수 있다.

연성 재료는 철근처럼 인장과 압축이 자유로우며 항복강도가 존재하는 재료들을 말한다. 연성 재료의 응력-변형율 선도는 위에서 설명한 그래프와 거의 일치한다. 이러한 연성 재료는 기준 강도가 항복 응력이기 때문에, 설계 할 때 항복 응력을 허용 응력(설계자가 지정, 실제로 현장에서 가해는 응력보다 조금 크게 설정된다.)으로 나눈 값을 '안전율'이라고 하고, 안전율이 높을수록 의외의 상황에 따른 과부하를 잘 견딜 수 있다.

취성 재료는 유리, 콘크리트, 세라믹, 지구의 지표면처럼 항복강도가 존재하지 않는 재료들을 말한다. 이러한 재료들은 탄성 구간을 넘어 소성구간에 접어들면 거의 즉시 파괴된다. 취성 재료의 응력-변형율 선도는 탄성구간밖에 존재하지 않으며, 항복 응력이 거의 극한 강도와 동일하다. 따라서 기준 강도 또한 극한 강도이다. 변형이 일어나면 변형이 한 지점에서 집중적으로 일어나다가 변형이 집중적으로 일어난 부분이 파괴되며 그 부분을 중심으로 균열이 생기는 연성 재료와는 달리, 변형이 재료 전체에서 일어나다가 파괴가 되는 순간 축적되어 있던 탄성 에너지가 재료 전체로 퍼지며 균열이 빠르게 확산되는 것이 특징이다. 이런 균열이 시작되는 지점은 표면에 흠(flaw)이 가거나 내부에 공동(void)이 생기는 등의 이유로 응력이 집중/증폭(stress concentration)되는 지점으로, 재료 전체에서 구조적으로 가장 취약한 부분에서부터 파괴가 시작된다. 이는 사슬을 팽팽하게 당길 때 가장 약한 고리가 가장 먼저 끊어지는 것(weakest link)으로 비유할 수 있다.

3.2 응력과 단층

지진이 일어나는 원인에 대한 가설 중 가장 유력한 가설 중 하나인 탄성반발설에서는 단층이 힘에 의해 탄성 에너지를 축적하고 있다가 어느 부분이 파괴되는 순간 탄성 에너지가 퍼져 지진이 일어난다고 이야기한다.

또 지구과학 시간에는 단층이 생길 때 약 45도 각도로 암석이 잘라지며 단층을 만들어낸 힘이 인장력인지 압축력인지에 따라 정단층과 역단층으로 구분한다. 이 때 지각에 가해지는 인장력과 압축력은 지각의 판(혹은 플룸)에 의해 발생한다. 그런데, 어떻게 인장력과 압축력이 가해지는 힘과 45도 각도로 지각을 부술 수 있을까? 45도 각도로 파괴가 일어나려면 45도 각도로 전단 응력이 가해졌어야 하는데 말이다.

인장력을 받고 있는 긴 재료 막대를 생각해보자. 막대의 중간에서 중심축과 수직한 단면을 보면 그 단면에 작용하는 응력은 막대의 중심축에 평행한 방향일 것이다.

이번에는 단면을 다르게 잘라보자. 막대의 중간에서 중심축과 수직한 단면에서 p 만큼의 각도만큼 기울어진 단면을 보면, 그 때의 응력도 중심축에 평행한 방향이다. 하지만, 우리는 이 응력을 각 p 만큼 기울어진 단면에 수직한 방향의 응력과 단면에 수평한 방향의 응력, 즉 전단 응력으로 분해할 수 있다. 지금 상황을 이해하기 위해, 직사각형과 그 위에 대각선 하나가 그어진 상황을 생각하고 직사각형을 기울여서 한 변은 경사지게 자른 단면과 접하게, 다른 한 변은 수직하게하고 대각선이 중심축과 수평하게 조정하면 그림이 나온다. 가장 긴 대각선은 중심축에 수평방향으로 작용하는 실제 응력이고, 우리는 지금 이 응력을 단면에 접하여 작용하는 전단응력과, 단면에 수직하여 작용하는 법선응력으로 분해하여 생각하는 것이다.

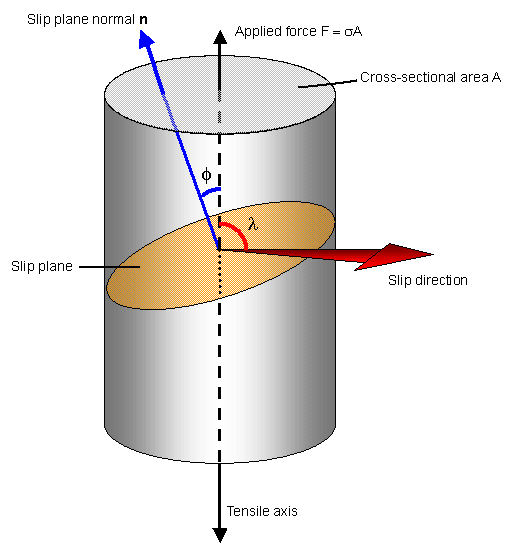
이렇게 생각하면, 막대의 매 단면은 실제로는 중심축과 수직한 방향으로, 즉 잡아당기는 방향으로 인장응력을 받고 있지만 이러한 응력들이 재료 내부에서는 재료를 비스듬한 방향으로 법선 응력을 작용하면서 비스듬한 방향으로 전단 응력을 작용하는 효과를 내고 있다는 것을 알 수 있다.

이 때 응력이 재료의 비스듬한 방향으로 전단 응력을 작용하는 효과는 비스듬한 각도가 45도일 때 가장 크다. 따라서 인장 응력 혹은 압축 응력이 매우 강할 때 재료 내부는 중심축에서 45도 기울어진 각도에서 가장 강한 전단응력을 받고 있는 것이다. (각도가 45도인 이유는 재료의 결정 구조와 그 결정 구조가 갖는 미끄럼계(Slip System)와 연관이 있다. )

전단 응력의 설명에서 나왔듯이, 전단 응력은 가위같은 것으로 물체를 자를 때 나타나는 응력이다. 따라서 이 전단 응력에 의해 재료는 45도 각도로 잘려나가게 된다.

판 구조 운동에 의해 인장력과 압축력을 받으면서, 지각도 비슷한 상황을 겪게 된다. 이 때문에 판 운동에 의한 인장/압축력이 강해지면 지각이 45도 각도로 부러지면서 단층을 형성하게 되는 것이다.

직접 실험해 보고 싶다면 분필을 다양한 방법으로 분질러 보면 된다.
1. 양 끝을 잡고 다른방향으로 비틀어 보는 방법.(비틀림 응력)
2. 양쪽끝을 평행하게 당겨보는 방법.(인장 응력)
3. 양쪽끝을 잡고 부러진 단면이 위나 아래를 향하도록 수직하게 힘을 주는방법(휨 응력)
각각의 방법에 따라서 부러지는 단면의 각이 다르게 나타나게 된다.

4 맥스웰 변형 텐서

만일 외부에서 작용하는 힘이 전자기력이라면 그 물체에 작용하는 응력은 다음과 같이 굉장히 복잡하게 나타난다.

[math]\sigma_{ij}\equiv \epsilon_{0}\left ( E_{i}E_{j} - \frac{1}{2} \delta_{ij} E^{2} \right ) + \frac{1}{\mu_{0}} \left (B_{i}B_{j}- \frac{1}{2}\delta_{ij}B^{2} \right )[/math]

자세한 것은 항목 참조.

기계과라 다행이다