- 관련 문서 : 수학 관련 정보
복면가왕의 출연자에 대해서는 피타고라스의 정리(복면가왕) 문서를 참조하십시오.
1 개요
450px
직각삼각형의 3개의 변을 a,b,c[1]라 하고 c에 대한 각이 직각일 때, a²+b²=c²으로 됨을 뜻하는 것으로서, 고대 그리스의 피타고라스가 처음으로 증명했다고 하여 피타고라스의 정리라고 한다.[2] 줄여서 FLT(2)로 쓰기도 한다(사실 이것은 페르마의 대정리의 함수 표현이긴 하지만).
피타고라스는 이 정리를 발견한 후 기쁨에 가득차 신에게 감사의 제사를 지냈다는 기록까지 존재한다. 이 때문에 자연수의 비, 즉 분수로는 표현할 수 없는 무리수의 존재가 증명되었다.[3] 그 후 피타고라스 학파는 혼란에 빠졌다. 피타고라스 학파가 거의 종교 단체 수준이었기에, 세상은 숫자(자연수)만으로 이루어졌다는 진리에 어긋난다는 이유로 함구하고 '신의 실수'로 만들어졌으며 없는 수로 취급하기로 했다. 그래서 실수에 포함된다 카더라 하지만 히파수스라는 제자가 세상에 알리려다가 참수당했다느니 수장당했다느니 하는 이야기도 있다.[4]
한국 기준으로 중학교 3학년 2학기 때 배우는 수학의 진리 중 하나.
2 증명
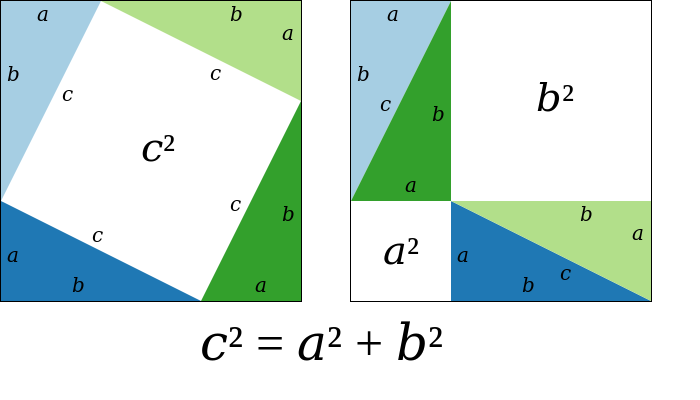 | x250px |
| 피타고라스 본인의 증명 | 유클리드의 증명[5] |
여러가지 증명법이 있다. 본문에 있는 것은 유클리드의 증명이며, 처음 봤을 때 직관적으로 이해하기 쉬운 방법으로는 바스카라의 증명이 꼽힌다.[6]
- 유클리드의 증명
- 페리갈의 증명
- 아나리지의 증명
- 바스카라의 증명
-
그냥 그려서 증명해보기
가장 많이 증명된 정리이기도 하다. 피타고라스의 정리들 증명만 모아놓은 책도 있을정도.
혹시 다른 증명법이 있으면 학계에 발표해보자. 자신의 이름을 따서 증명법을 만들어줄 것이다. 하지만 이게 말처럼 쉬운 건 아닌 게, 지금까지 피타고라스의 정리를 증명하는 방법으로 알려진 것만 400개가 넘어간다.# 그리고 이 방법 중에는 제임스 가필드 20대 미국 대통령이 발견한 것도 있다.[7][8]
그뿐만 아니라 정리의 '역'도 성립하는 명제중 하나다. 즉, 삼각형이 직각이라는 것과 저기 위에 식이 성립한다는 것과는 완벽하게 성립한다. 이게 역이 성립한다는 건 피라미드가 세워질 때부터 세계 거의 모든 문화권에서 귀납적으로 알려져 있었지만 연역적으로 증명하는 건 은근히 어렵다. 당신이 중학교 수학 영재반 이상의 실력이라면 한번 도전해보자.
고등학교 미적분2 교과서 내에는 없지만 가르치는 학교가 많은 코사인 제2법칙이란 것이 있다. 이 정리는 '피타고라스 정리의 일반화'라고 평가되어 있다. 쉽게 말하자면 피타고라스 정리 확장팩. 모든 삼각형에 대해 성립하는 법칙이다. 위 그림의 기호를 그대로 붙이면 c2 = a2 + b2 -2ab*cosC. C=90도일때 이 식은 피타고라스의 정리가 된다.
발전형이 있다. 드 가의 정리라는, 3면이 직각삼각형이고 직각인 꼭짓점이 한 점에 모이는 삼각기둥에서 각각 세 직각삼각형의 넓이의 제곱의 합이 나머지 한 삼각형의 넓이의 제곱의 합이라는 버전.
일반적인 유클리드 공간 [math]\mathbb{R}^n[/math]에서 m(m<n)차원 르베그 가측인 부분집합 [math]S[/math]가 있을 때 [math]\mathbb{R}^n[/math]의 표준기저(standard basis)에서 m개의 원소를 뽑아 만들 수 있는 부분공간 [math]W_1, W_2, \cdots, W_x[/math]에 대하여([math]x= _nC_m[/math]) [math]S[/math]의 [math]W_i[/math]로의 정사영을 [math]S_i[/math]라고 할 때, [math]\displaystyle \mu \left(S\right)^2=\sum_{i=1}^{x}\mu \left(S_i\right)^2[/math]가 성립한다. Donald R. Conant와 William A. Beyer가 증명하였다.
참고로 피타고라스의 정리는 유클리드 기하학에서만 성립한다. 예를 들어, 구의 표면에 직각삼각형을 그렸을 때에는 피타고라스의 정리는 성립하지 않는다. 유클리드 제5공준의 다른 표현이 피타고라스의 정리란 말도 있는 이상 당연한 결론. 애초에 구면 위에선 모든 각이 직각인 삼각형도 아무렇지 않게 그릴 수 있다.
3 활용
"증명" 자체는 고대 그리스에서 이루어졌지만, 직각삼각형의 3변 길이 공식 자체는 3800년 전 메소포타미아의 라르사에서 발견된 점토판 Plimton 322(1820–1762 BC)에서 이미 등장했다.#. 중국에서는 3000여년 전에 진자란 사람에 의해 '구고현의 정리'로 독자적으로 발견했다. # 한나라 때의 주비산경에는 구고멱합이성현멱이라고 해서 그걸 일반화하기도 했고 해도산경[1]에는 상당히 수준 높은 문제가 나오기도 했다.양판소와 다르게 고등학교 졸업 정도로는 삼국시대 수준의 문명에서도 뛰어난 학자는 될 수가 없다. 과거 사람들은 지식과 도구, 의무 교육이 없었던 것뿐이지. 머리가 엄청 뒤떨어진 것이 아니다.
참고로 [math]c^2 = a^2 + b^2[/math]를 만족하는 수를 피타고라스 수(pythagorean triple)라고 하는데 이 피타고라스의 방정식을 만족시키는 자연수의 순서쌍은 무한히 존재한다.[9] 하지만 cn = an + bn 에서 n이 3이상으로 올라가면 이 방정식을 만족시키는 자연수의 순서쌍은 하나도 찾을수가 없는데, 전세계의 수학자들이 수백년간 이걸 증명할수가 없었다. 더 자세한 이야기는 페르마의 대정리에서 보자.
피타고라스 수는 이글루스의 덧글 차단 기능과 관련있는 내용이기도 하다(...)
[math]Win = \frac{runs \quad scored^2}{runs \quad scored^2 + runs \quad allowed^2} = \frac{1}{1 + (runs \quad allowed / runs \quad scored)^2}[/math]
야구를 원자단위로 분해하는 것을 업으로 하는 세이버메트릭스에서는 팀의 득실점을 가지고 시즌 승률을 예측하는 공식을 개발했는데, 그 공식의 생김새가 피타고라스의 정리와 닮았다 하여 피타고라스 승률, 피타고리언 승률이라 부른다. 공식은 위와같은데 해석을 하자면 득점의 제곱/(득점의 제곱+실점의 제곱)이다
우리나라에서는 천문학자 남병길이 이를 이용한 유씨구고술요도해라는 수학서를 저술했으며, 이 이론을 통해 숭례문, 원각사지 십층석탑, 경복궁 등을 만드는 데도 사용되었다.
- [math]\displaystyle \sqrt{\begin{bmatrix} 1 \quad 0 \ 0 \quad 1 \end{bmatrix}} = {1 \over h} {\begin{bmatrix} b \quad a \ a \quad -b \end{bmatrix}}, {1 \over h} {\begin{bmatrix} -b \quad -a \ -a \quad b \end{bmatrix}}, {1 \over h} {\begin{bmatrix} -b \quad a \ a \quad b \end{bmatrix}}, {1 \over h} {\begin{bmatrix} b \quad -a \ -a \quad -b \end{bmatrix}}, \begin{bmatrix} 1 \quad 0 \ 0 \quad 1 \end{bmatrix}, \begin{bmatrix} 1 \quad 0 \ 0 \quad -1 \end{bmatrix}, \begin{bmatrix} -1 \quad 0 \ 0 \quad 1 \end{bmatrix}, \begin{bmatrix} -1 \quad 0 \ 0 \quad -1 \end{bmatrix} [/math]
- ↑ a,b,h라고 쓰기도 한다.
- ↑ 피타고라스가 실제로 이 정리를 증명했는지는 불확실하다. 피타고라스와 동시대 사람들의 기록에는 피타고라스의 수학적 업적에 대한 내용이 없다.
- ↑ 어떤 수가 무리수인가는 몰랐다. 그냥 단지 '어? 왜 어떤수를 제곱해서 2가 나오지를 않지?' 라는 식으로 '아! 유리수가 아닌 수가 있는거구나' 라는 수준의 추론이기 때문이다. 정확하게 무리수임을 증명한것으로 기록에 남는것은 유클리드의 증명. 흔히 아는 대표적인 귀류법을 이용한 증명중 하나이다.
- ↑ 정확히는 신념과 어긋나는 사실을 발견했다는 이유로 비밀을 지키기 위해 죽였다고 한다.
- ↑ 뭔가 중간에 휙 건너띈 증명이지만... 삼각형 KAB 와 삼각형 CAD의 같음을 이용해서 사각형 ADML와 KACH가 면적이 같음 그리고 같은 원리로 CBFG와 LMEB가 같음을 증명하는 유클리드 증명이다.
- ↑ 어떤 정사각형의 네 변을 a:b의 비율로 나눈 후, 나누어진 네 점을 잇는 한 변의 길이가 c인 새로운 정사각형을 그려서 원래 정사각형을 새로운 정사각형과 4개의 합동인 삼각형으로 구분하고, "원래 정사각형의 넓이 = 새로운 정사각형의 넓이 + 삼각형 4개의 넓이"임을 이용하여 증명하는 방법. 유클리드 증명법과 함께 중학교 수학 피타고라스의 정리 단원에서 다룬다.
- ↑ 이 네임밸류 때문인지 교과서나 참고서에 이 방법이 같이 실려있는 경우가 있다(...)
- ↑ 그런데, 사실 가필드의 증명에 등장하는 사다리꼴을 뒤집어 붙이면 완벽하게 피타고라스의 증명이다. (...)
- ↑ 심지어 공식도 존재한다. 근데 유도과정을 보면 분명이 고등학교 과정 이내인데도 정신이 저 멀리 날라가는 느낌을 들게 할수있다. 궁금하면 수학소설 수학걸2 참고.