- 상위 문서: 정다포체
| 4차원 볼록 정다포체 | |||||
| 정오포체 | 정팔포체 | 정십육포체 | 정이십사포체 | 정백이십포체 | 정육백포체 |

회전하는 정오포체의 3차원 투영 모습[1].
1 개요
正五胞體/5-cell, 또는 Regular pentachoron(복수는 Pentachora)
한 개의 모서리에 세 개의 정사면체가 만나고, 총 다섯 개의 정사면체으로 이루어진 정다포체. 4차원 단체(4-simplex)로, 밑면이 정사면체인 4차원 초뿔(tetrahedral pyramid)이다.
정오포체 6개를 한 면에 3개씩 만나게 만드는 방식으로 이어 붙여 5차원 도형인 5-단체(5-simplex, 또는 헥사테론(Hexateron))을 만들 수 있다.
2 정오포체에 대한 정보
| 단위/특성 | 개수 | 비고 |
| 슐레플리 부호 | {3,3,3} | |
| 꼭지점(vertex, 0차원) | 5 | |
| 모서리(edge), 1차원) | 10 | |
| 면(face, 2차원) | 10 | 정삼각형 |
| 입체(solid, 3차원) | 5 | 정사면체 |
| 쌍대 | 정오포체 {3,3,3}[2] | |
| 포함 관계 또는 다른 이름 | 엇정삼각기둥(Triangular antiprism) 4차원 단체(4-Simplex) 정사면체 초뿔(Tetrahedral pyramid) |
한 변의 길이가 [math]a[/math]인 정오포체가 있을 때
초뿔로서의 높이[3] = [math]\displaystyle\frac{\sqrt{10}}{4}a[/math]
총 모서리 길이(total edge length) = [math]10a[/math]
총 면적(total surface area) = [math]\displaystyle\frac{5\sqrt{3}}{2}a^2[/math]
겉부피(surcell volume) = [math]\displaystyle\frac{5\sqrt{2}}{12}a^3[/math]
초부피(bulk) = [math]\displaystyle\frac{\sqrt{5}}{96}a^4[/math]
2.1 3차원 투영 모습
- 한 꼭지점 중심으로 투영된 모습은(Vertex-first projection) 정중앙을 중심으로 사등분된 정사면체의 모습이다. 이 때 네 개의 입체가 보이며, 나머지 한 개의 입체는 가려져서 보이지 않는다. [4]

- 한 모서리를 중심으로 투영된 모습은 (Edge-first projection) 중심축을 중심으로 삼등분된 삼각쌍뿔의 모습이다. 이 때 세 개의 입체가 보이며, 나머지 두 개의 입체는 가려져서 보이지 않는다.

- 한 면을 중심으로 투영된 모습은 (Face-first projection) 적도를 중심으로 이등분된 삼각쌍뿔의 모습이다. 이 때 두 개의 입체가 보이며, 나머지 세 개의 입체는 가려져서 보이지 않는다.
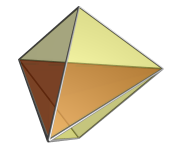
- 한 입체를 중심으로 투영된 모습은(Cell-first projection) 온전한 정사면체의 모습이다. 나머지 네 개의 입체는 뒤에 있기 때문에 가려져서 보이지 않는다.
