平行 / parallel
1 개요
| = |
| 등호의 모양은 평행선에서 비롯되었다. |
평행이란, 어떤 평면에서의 직선이나 공간에서의 평면을 한없이 늘려도 영원히 만나지 않는 상태를 말한다.[1] 다만 이건 유클리드 기하학에서만 한정되며, 비유클리드 기하학은 평행선 공준을 부정하는 것으로부터 시작하기 때문에 평행선이 존재하지 않거나, 평행선이 여러 개 존재한다. 아래 성질들은 유클리드 기하학에 한한다.
직선이거나 평면인 한 도형 [math]l[/math]과 다른 도형 [math]m[/math]이 서로 평행할 때 수학에서는 [math]l[/math] ∥ [math]m[/math]라는 식으로 표현한다.
평형과 발음이 비슷하여 서로 혼동할 수 있으니 주의하자. 평형은 미시적으로는 수많은 요소들이 각자 운동하고 있지만 거시적인 양은 변하지 않는 상태를 의미하고 순수한 수학보다는 물리학과 경제학 등에 더 많이 사용되는 용어이다.
2 성질
2.1 유클리드 기하학적 성질
- 서로 평행한 두 직선에 교차하는 또 다른 직선을 그렸을 때 엇각, 동위각 등의 크기가 같다. 이에 대한 증명은 각 문서 참조.
- 서로 평행한 두 직선은 어느 점을 기준으로 삼아도 다른 직선까지의 거리가 같다.
- 직선 [math]l[/math]과 직선 밖의 점 [math]P[/math]에 대하여, [math]l[/math]과 평행하고 [math]P[/math]를 지나는 직선은 단 하나밖에 없다(유클리드 제 5공준의 변형).
이러한 성질을 활용하여 한 직선의 평행선을 작도할 수 있다.
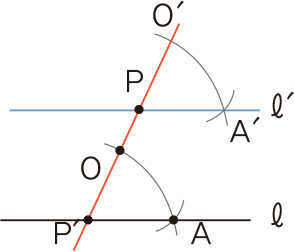
- 직선 [math]l[/math] 있을 때, 그 위에 있지 않은 점 [math]P[/math]을 그린다.
- 점 [math]P[/math]를 지나고 직선 [math]l[/math]과 한 점에서 만나는 직선을 그리고, [math]l[/math]과 만나는 점을 [math]P[/math]′라고 한다.
- 점 [math]P[/math]에 컴퍼스를 대고 원을 그린다. 이때 원이 직선 [math]\overline{PP}[/math]′와 만나는 점을 점 [math]O[/math]라고 하고 원과 직선 [math]l[/math]이 만나는 점을 점 [math]A[/math]라고 한다.
- 방금 3번에서 그린 원과 같은 반지름으로 점 [math]P[/math]에 컴퍼스를 대고 원을 그리고, 이 원과 직선 [math]\overline{PP}[/math]′가 만나는 점을 [math]O[/math]′라고 한다.
- 컴퍼스로 점 [math]O[/math]와 점 [math]A[/math]의 거리를 재고 그 길이를 반지름으로 하여 점 [math]O[/math]′에 컴퍼스를 놓고 원을 그린다. 이 원과 4번에서 그렸던 원을 교점을 [math]A[/math]′라고 한다.
- 점 [math]P[/math]와 점 [math]A[/math]′를 연결하는 직선 [math]l[/math]′을 그린다. 이로써 직선 [math]l[/math]의 평행선인 직선 [math]l[/math]′을 그렸다.
2.2 벡터적 성질
영벡터가 아닌 두 평면벡터 [math]a[/math]와 [math]b[/math]가 이루는 각을 θ(0≤θ≤π)라고 할 때 [math]a[/math] • [math]b[/math] = |[math]a[/math]| |[math]b[/math]| [math]cos[/math]θ인데, θ의 값이 0이면 [math]a[/math]와 [math]b[/math]는 서로 평행하면서도 방행이 서로 같고, θ의 값이 π이면 서로 평행하면서도 방향은 서로 정반대이다. 이 역 또한 성립되며, 이를 식으로 표현하면 다음과 같다.
[math]a[/math] ∥ [math]b[/math] ↔ [math]a[/math] • [math]b[/math] = ± |[math]a[/math]| |[math]b[/math]|
또는 영벡터가 아니고 정확히 일치하지 않는 두 벡터간에 0이 아닌 실수배 관계가 존재하면 평행으로 볼 수도 있다.
평행인 두 벡터를 외적하면 0이고, 내적하면 두 벡터의 절댓값의 곱이다.
3 수학 외의 용례
널리 알려진 수학 용어라, 일상적인 용례에서도 쓰이곤 한다. "평행선을 달리다"라는 관용어가 대표적인 예로, 협상 등에서 아무런 접점도 없이 허송세월하는 것을 뜻한다.
3.1 활용
- 직진 도로의 차선은 특수한 상황이 없는 경우 평행하게 만든다.
- 도로가 등에 차들을 일직선으로 주차시키는 것을 평행주차라고 한다.
- 평행봉은 철봉 2개를 평행으로 배치한 도구이다.
- 착시현상을 보여주는 소재로 잘 활용된다. 기하 도형 주변에 특정한 변화를 가하면 시각 자극이 과도하게 수용되어 실제 도형과 다른 뒤틀림 현상이 일어나는데 평행선은 두 개의 곧은 직선만으로 이루어졌다는 명확한 시각 정보를 가지고 있어 그 직선이 아닌 다른 시각 자극을 주면 그것을 뒤틀리도록 하기 쉽기 때문이다. 평행선을 이용한 착시 현상에는 다음과 같은 예가 있다.
 | 체르너 착시 (Zollner illusion) 평행선 위에 여러 개의 빗금을 긋되 한 선 위에 그어지는 빗금은 서로 평행하게 하며 빗금 간 거리를 일정하게 유지하고, 다른 선 위의 빗금은 옆의 선에 그어진 빗금과 수직이 되도록 그으면 평행선이 휘어 보인다. |
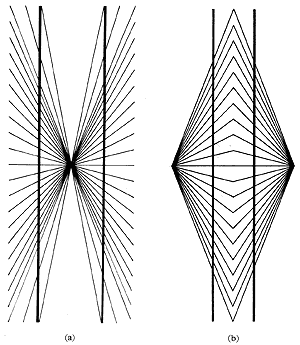 | 헤링 착시와 분트 착시 (Herring illusion & Wundt illusion) 서로 평행한 두 직선 사이 한가운데에 방사선을 그으면 두 평행선이 바깥으로 휘어 보인다. 반대로 평행선 바깥쪽에 각각 방사선을 그으면 두 직선이 안으로 휘어 보인다. |
| 파일:Attachment/Opticalillusion01.gif | 카페 월 착시 (Cafe Wall illusion) 서로 간의 거리가 같은 평행선 여러 개 사이에 변의 길이가 평행선 간의 거리와 정사각형들을 그리고 위아래로는 서로 어긋나게 배열하고 좌우로는 흑백이 교차되도록 하면 평행선들이 휘어 보인다. 이 때 일반적으로 검은색 칸이 더 바깥쪽으로 나온 곳은 평행선끼리의 거리가 더 멀고 안으로 들어간 곳은 거리가 가까워 보인다. |
- 평행우주 혹은 평행세계, 평행차원은 보통 다중우주를 일컫는 용어로 사용되는데, 이는 우리가 살고 있는 우주가 아닌 다른 시공간에 존재하는 우주를 뜻하는 말로 각 우주가 차원의 벽으로 나뉘어 있어 영원히 만날 수 없는 점이 평행선을 연상시키기 때문에 사용된 용어이다.