페르마의 마지막 정리

• 관련 문서: 수학 관련 정보, 피에르 드 페르마, 앤드루 와일스, 나무위키/특징적 표현, 더 이상의 자세한 설명은 생략한다

Quaestio VIII. Propositum quadratum dividere in duos quadratos. Imperatum sit ut 16. dividatur in duos quadratos. Ponatur primus 1Q. Oportet igitur 16. - 1Q. aequales esse quadrato. Fingo quadratum a numeris quotquot libuerit, cum defectu tot unitatum quod continet latus ipsius 16. esto a 2N. - 4. ipse igitur quadratus erit 4Q. + 16. - 16N. haec aequabuntur unitatibus 16. - 1Q. Communis adiiciatur utrimque defectus, et a similibus auferantur similia, fient 5Q. aequales 16N. et fit 1N. 16/5. Erit igitur alter quadratorum 256/25. alter vero 144/25. et utriusque summa est 400/25. seu 16. et uterque quadratus est. Observatio domini Petri de Fermat. Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet. 문제 8. 제곱수를 두 제곱수로 나누기 위해. 문제가 16을 두 제곱수로 나누는 것이라고 하자. 먼저 x²을 둔다. 그러면 16-x²이 제곱수여야 한다. 임의의 수에서 제곱해서 16이 되는 수를 뺀 것(2x-4라고 하자)에 제곱의 형태를 취하자. 2x-4의 제곱은 4x²-16x+16인데 이를 16-x²과 같다고 한다. 양쪽에서 공통으로 모자란 부분을 더하고 같은 양만큼 없애면(즉 양변을 정리하면) 5x²=16x가 되고, x=16/5가 된다. 따라서 하나를 256/25로 하고 다른 하나를 144/25로 두면 그 합은 400/25, 즉 16이 되고 둘은 각각 제곱수다. 피에르 드 페르마 경의 관찰 하지만 세제곱수를 두 세제곱수로, 혹은 네제곱수를 두 네제곱수로, 또 일반적으로 제곱보다 큰 거듭제곱수를 동일한 지수의 두 거듭제곱수로 나눌 수 없는데, 나는 이에 대한 실로 놀라운 증명법을 발견했다. 하지만 그걸 여기다 적기에는 책의 여백이 너무 부족하다.

1 개요

알기 쉽게 정리 해놓은 만화

페르마의 마지막 정리(Fermat's Last Theorem, FLT)는 '방정식 [math]x^n + y^n = z^n[/math] ([math]n \gt 2[/math]인 자연수)에는 자명하지 않은 정수 해의 쌍 ([math]x[/math], [math]y[/math], [math]z[/math]) 값이 존재하지 않는다.' 라는 수학정리를 일컫는 말이다. 단, 여기서 '마지막'이란 것은 페르마가 마지막으로 내놓은 정리가 아니라 마지막까지 증명되지 않았던 정리라는 의미다.

2 소개

페르마는 증명하지 않았기 때문에 엄밀히 말하면 페르마의 추측이라고 부르는 것이 옳다. 그러나 페르마가 자신이 증명해 냈다는 주장을 존중하여 일반적으로 페르마의 정리라고 부른다. 이 정리는 20세기를 넘기기 직전인 1995년 영국의 수학자 앤드루 존 와일스 경(Sir Andrew John Wiles)에 의해 증명되었다.

수학 역사에서 존재했던 여러가지 난제들 중 가장 유명한 난제인데 누가 봐도 겉보기에는 아무 것도 아닌 지문인데도 불구하고 장장 400년에 가까운 세월 동안 전 세계 유수한 수학자들을 골로 보내버렸기 때문이다. 수학계에서 난제들은 수도없이 많지만 페르마의 마지막 정리는 굉장히 간결명료한 수식과 문장으로 구성되어있어 일반인들에게도 이해가 쉬워 다른 난제들보다도 널리 알려졌다. 하지만 이 간단한 수식 하나를 증명하는데에는 페르마 이전의 수학부터 페르마 사망 이후 350여년 동안 전세계 인류가 추가로 쌓아올린 수학까지, 수학이라는 학문의 정수가 총동원됐다.

3 정리의 어려움

3.1 기원

수학왕 피에르.D.페르마 이 자가 남긴 문제는 작은 중장년 아재인 앤.D.류-와일즈 란 아재가 풀어냈는데....

프랑스의 수학자 피에르 드 페르마는 자신의 연구 결과를 출판하려는 시도를 하지 않았고 스스로 알아낸 것만으로 만족했기 때문에 그가 다른 수학자들과 주고받은 편지에서 소개한 일부의 내용에 포함되지 않는 연구 내용은 대부분 알려지지 않았다. 그의 사후 그의 장남인 클레망사뮈엘(Clément-Samuel)은 페르마가 디오판토스의 정수론 책인 아리스메티카에 낙서처럼 달아놓은 주석을 정리해서 책으로 출판했고, 이를 통해서 페르마가 한 연구가 밝혀졌다. 아리스메티카에서 임의의 제곱수를 서로 다른 두 제곱수의 합으로 표현하는 문제에 달아놓은 주석이 바로 페르마의 대정리다.

이 문제는 피타고라스의 삼각수와 관련된 문제, 즉 방정식 [math]x^2 + y^2 = z^2[/math]을 만족하는 해 (x, y)를 z에 관하여 나타내는 문제다. 위 방정식을 만족하는 해는 어떤 정수 a, b 에 대해서 [math](x, y, z) = (a^2 - b^2 , 2ab , a^2 + b^2 )[/math] 혹은 그들의 [math]k[/math]배라는 것을 고등학교 수준에서 비교적 쉽게 풀어서 알 수 있다. 따라서 [math](x, y)={(a^2 - b^2 )/(a^2 + b^2 ) * z , (2ab)/(a^2 + b^2 ) * z}[/math]로 나타낼 수 있다. 아리스메티카에서 제시하는 해는 여기서 [math]b=1[/math]을 대입한 값인 [math](x, y)={(a^2 - 1)/(a^2 + 1) * z , (2a)/(a^2 + 1) * z}[/math]다.

[math]a[/math]와 [math]b[/math]는 임의의 정수이므로, 이 해는 무한히 많게 된다. 그런데 페르마는 이 문제 부분에 지수가 3 이상일 경우에는 유리수 해가 없다고 주장하면서도 이것을 증명하는 대신 "더 이상의 자세한 설명을 생략"해버림으로써 장장 300여년에 걸친 낚시가 시작되었다. 페르마는 어려운 문제를 증명하고는 지인들에게 증명에 대한 설명은 없이 '나 이거 증명했으니 풀어 봐라'는 식으로 말하는 것을 즐겼기 때문에 수학자들은 저 문제가 오래지 않아 해결될 것으로 생각했으나 어찌된 영문인지 아무리 해봐도 풀리지가 않았던 것.

수학 전공자뿐만 아니라 아마추어 수학 연구가들 역시 헤아릴 수 없을 정도로 많이 낚였다. 겉으로 보기에는 대단히 쉬워보이는 문제의 외형, 프로 수학자들도 손 들었다는 극악한 문제의 난이도, 그리고 17세기의 아마추어도 푸는 문제를 내가 못 풀 게 없다는 터무니없는 착각 등이 일을 크게 만든 것이다. 낚인 사람 중에는 자살한 사람, 정신이상이 생긴 사람, 심지어는 결투를 벌인 사람도 있다고 한다. 사실 갈루아가 만든 갈루아 군은 나중에 와일즈가 풀이에 이용하기 전까지는 페르마의 마지막 정리와 완전히 동 떨어졌고 에버리스트 갈루아 역시 페르마의 마지막 정리에 관심이 없었다.

3.2 초창기

문제가 알려진 후 한동안은 아무도 손을 대지 못했다. 오늘날에도 유명한 당대의 수많은 대 수학자들이 손을 댔지만, 그 누구도 정리를 증명해내지 못했다.

이때즈음 하여 단서를 발견한 수학자가 레온하르트 오일러다. 그렇다, 오일러의 정리로도 유명한 그 대수학자 오일러가 맞다. 그는 자료를 조사하기 시작했고, 곧 페르마 본인이 n=4일 때의 증명을 해 놓았다는 사실을 찾아냈다. 페르마 사후에 출판된 아리스메티카의 주석에 써있었는데, 다들 그것을 못 보고 지나쳤던 것이다. 비록 '여백이 좁다고' 제대로 증명을 끝내지 않았긴 했지만, 일정 수준의 수학자라면 누구나 그걸 보고 증명해낼 수 있을 정도로는 풀이를 해놨던 것이다.

이것을 토대로 오일러는 'n=3일때 정리는 성립한다'를 귀류법의 일종인 무한강하법으로 증명했다. 이 방법은 n=4일 경우에 사용되는 증명법과 본질적으로는 동일하다. 그러나 비슷한 방법으로 n=5일 때의 증명을 시도했으나 끝내 해내지 못했고, 페르마의 옛 집을 동료들까지 동원해서 샅샅이 뒤졌음에도 불구하고, 모든 n값의 증명은 찾아내지 못했다.

이후 많은 수학자들이 도전했지만, 별다른 성과는 나오지 않았다. 그 때 소피 제르맹(Marie-Sophie Germain) 이라는 여성 수학자가 등장했고, 당시로서는 여성은 수학같은 어려운 학문을 못 한다는 시선 탓에 여성 수학자 자체가 적었던 힘든 사회상에서 살았음에도 불구하고 성과물을 내놓았다. 소피 제르맹이 업적에 사용한 것은 소피 제르맹 소수와 소피 제르맹 정리이고 이 덕분에 골머리를 앓고 있던 n=소수인 경우의 상당부분이 증명되었다. 'n=5일때 성립한다'를 포함한 수많은 증명이 소피 제르맹의 발견을 이용해서 증명된 것이다.

그러나 결국 원론적인, 모든 n값이 성립하지 않는다는 것은 증명되지 못했다. 만약 'n=소피 제르맹 소수가 아닌 소수'라면 답이 없다는 거다. 수학자들이 어떻게든 노력해서 n=소수인 경우에도 증명이 가능하도록 하는 규칙을 찾아내기는 했지만, 그게 안 통하는 소수도 있었다. 그런 게 유한했다면 수작업으로 밤을 새든, 몇년간 붙잡든, 몇대에걸쳐 인해전술을 하든 어떻게 근성으로 증명할 수 있겠지만, 그런 소수가 무한개 있다는 문제가 있었다. (중학교 1학년 때 배우지만, 소수의 개수는 무한하고 소수를 늘어놓은 수열에서는 아무런 규칙이 성립하지 않는다.) 이 불행한 진실은 에른스트 쿰머(Ernst Eduard Kummer)가 증명했는데, 그는 n이 정규소수일 경우의 증명을 완성했지만 n이 비정규소수일 경우 하나하나 수작업으로 풀어야 한다는 사실을 발표했던 것이다.

덤으로 이 증명을 연구하는 과정에서 '[math]x^4 + y^4 = z^4[/math]은 양의 정수해를 갖지 않는다', '[math]x^4 - y^4 =z^2[/math]는 정수해를 갖지 않는다'등의 아류작들이 이 시기에 증명되었다. 이런 '아류작들'의 수는 매우 많아서, 그것만으로도 수학계에 충분히 공헌했다고 할 수 있다.

3.3 침체기

쿰머가 불편한 진실을 발표한 이후 점점 수학계에서 FLT에 대한 관심은 멀어져갔으며, 일부 수학자들은 이에 대해서 아예 페르마가 틀렸다 정도로 생각하게 되었지만 파울 프리드리히 볼프스켈이라는 의사이자 아마추어 수학자가 이 문제를 증명하는 사람에게 현상금 10만 마르크를 주겠다고 선언하면서 재야의 아마추어 수학자들에게도 이 문제가 알려지게 된다. 볼프스켈은 실연당한 후 자살할 생각이었는데, 자살할 시간을 정해놓고 책장을 뒤져보던 중 페르마의 정리를 발견하고, 페르마의 정리에 대해 전율을 느끼고 삶의 의미를 되찾게 되었다고 한다. 이에 그는 경의를 담아 페르마의 대정리를 증명하는 사람에게 10만 마르크를 주겠다고 약속했고, 그 상금은 괴팅겐의 왕립과학원에 기탁되어 <볼프스켈 상>이라고 정식 명명되었다. 수많은 이들이 상금을 위해서 해법을 투고하기 시작했지만 모든 증명이 기본적인 오류를 내포하고 있었고 아주 쌩뚱맞은 논리를 적어서 보낸 유사수학자들도 많았다.

대다수의 수학전공자들은 이 문제를 도외시하긴 했지만, 실제로는 자신이 없어서 그랬다고 봐야 할지도 모른다. 유명한 수학자인 다비트 힐베르트에게 왜 이 문제를 안 푸냐고 사람들이 묻자, "적어도 2년 이상의 시간을 투자해야 하지만 실패할 게 분명한 일에 그럴 순 없다." 고 답한 바가 있다. 한편 인류가 발전하고 점차 하나의 교통권으로 묶이자, 국가별로 고유의 수학체계를 가지고 있던 나라들이 서양에서 정리한 수학과 접촉하게 되면서 전체 수학 인구가 폭증하여 학문의 발전속도가 과거와는 비할 바 없이 빨라졌으나 여전히 페르마의 마지막 정리만큼은 그 어느 대륙과 국가의 수학자들이라 하더라도 도저히 해결책을 찾지 못했다. 이렇게 FLT의 명성이 차차 높아지면서 대중매체에서도 '절대로 풀릴 수 없는 난제'로서의 출연도 많아졌다. 아서 포기스의 1957년작 단편소설 '악마와 사이먼 플래그'에서는 악마와 외계인(편미분방정식을 암산으로 푸는 외계인이었다.)이 이 문제에 도전했다가 실패했다. 당시 사람들이 페르마의 마지막 정리를 어떻게 생각했는지를 알려주는 예다.

20세기 중후반기에 개발된 컴퓨터로도 이 문제를 풀지 못한다. 숫자 n은 무한히 많기 때문에 하나하나 계산할 수도 없기 때문이다. 결국 페르마의 마지막 정리는 정말 아무도 풀지 못하는 미지의 문제라고 여겨지게 되었다.

3.4 전환기

페르마의 정리가 증명되는 데는 말 그대로 현대수학의 모든 것이 필요했다. 와일즈가 이를 증명하는 데는 "모듈러성 정리"가 결정적인 역할을 했다. 이 모듈러성 정리는 수학의 다양한 분야에서도 서로 연관성이 있다고 생각하기 어려운 분야들의 다리 역할을 함으로서 당시에는 '만약 모듈러성 정리가 사실이라면' 이라는 전제 하에 나온 논문들이 많았다. 따라서 모듈러성 정리를 증명하는 것은 페르마의 정리를 증명하는 것뿐만이 아니고 사상누각과 같았던 새로운 수학 분야의 근간이 되는 것이었다. 게다가 이를 증명한다면 대통일 수학이라는 궁극적인 목표에 도달한 첫 번째의 업적이 될 것이 확실했다.

그런데 수학자 게르하르트 프라이가 페르마의 정리를 타원곡선의 형태로 변형을 시켰는데 이 식은 페르마의 정리가 틀렸다는 가정 하에 유도된 식이었다. 이를 통해서 프라이는 모듈러성 정리가 맞는다면 프라이가 유도해낸 타원곡선이 존재하지 않는 것을, 따라서 페르마의 정리를 만족하는 정수해가 존재하지 않는 것을 보였다. 즉 프라이는 모듈러성 정리를 증명하면 페르마의 정리 또한 부록으로 증명된다는 점을 증명한 것이다. 다만 프라이의 증명 과정에는 일부 완성되지 않은 부분이 포함되어 있었고, 그렇기에 이 증명은 엡실론 추측(Epsilon conjecture)으로 명명되었다.

프라이가 이 사실을 밝혀내기 전까지 프로 수학자들은 페르마의 마지막 정리가 어렵기만 하고 수학적으로는 별로 중요하지 않다며 관심이 없는 척 했지만, 프라이가 발표한 엡실론 추측을 통해 페르마의 마지막 정리를 정복할 가능성이 보였다는 소식을 들은 순간 마하 100으로 달려와서 논문 내용을 복사해갔다. 헌데 기다렸다는 듯이 풀리지 않아 모두를 좌절시켰으나, 케네스 리벳(Kenneth A. Ribet, 통칭 켄 리벳)이라는 수학자가 고생 끝에 엡실론 추측을 완성하는 순간, 전 세계 수학계는 드디어 페르마의 대 정리를 정복할 수 있다며 흥분했다. 이를 통해 엡실론 추측은 리벳의 정리(Ribet's theorem)이라는 새 이름을 얻었으며, 리벳은 이 추측을 증명한 업적으로 1989년에 페르마 상(Fermat Prize)을 수상했다.

3.5 최초의 발표

드디어 지난 400년간의 좌절을 끝낼 한줄기 희망 앞에, 수많은 수학자들이 도전을 시작했다. 허나, 이 희망은 새로운 절망을 위한 운명의 포석에 불과했다. 막상 타니야마-시무라의 추론이 증명되지 않았던 것이다! 결국 사람들은 페르마의 정리를 증명하는 것을 포기하기 시작했으며, 켄 리벳도 마찬가지였다. 그러나 포기하지 않은 사람이 있었으니 그가 바로 앤드루 와일즈.

와일즈는 석사 학위를 이수한 후 '타원곡선'에 대한 내용을 이수했는데, 당연하게도 그때는 페르마의 마지막 정리와 타원곡선은 아무런 관련이 밝혀진 바 없었다. 그러니까 정말로 운이 좋게도 페르마의 마지막 정리 증명에 기초를 쌓은 것이다. 그리고, 페르마의 마지막 정리에 도전한 와일즈는 7년동안 은둔형 외톨이처럼 자기 집 다락방에 처박혀서 연구에만 몰두를 시작했으며, 이런 와중에도 강의 준비 등 가르치는 일에는 충실했다고 한다. 거기에 다른 수학자들의 관심을 돌리기 위해서 다른 연구를 계속하고 있는 것처럼 위장할 목적으로 논문을 미리 작성해 놓고 6개월 간격으로 제출했다고 한다. 다만 그의 아내와, 논문의 검토를 맡았던 동료 교수 닉 카츠(Nick Katz)만이 그 비밀을 알고 있었다.

각고의 연구 끝에 그는 듣기만 해도 정신을 4차원으로 보내버리는 현대수학을 총동원하여 시무라의 추론을 증명했고, 결과적으로 페르마의 정리를 증명해냈다. 다만 와일즈 교수가 이때 증명한 것은 준안정 상태의 경우 뿐이었으나, 이것만으로도 페르마의 정리를 증명하기에는 충분했다. 추가로, 완전한 타니야마-시무라의 추론의 증명은 1999년에 리처드 테일러(와일즈 교수의 제자)와 다른 수학자들의 공동연구로 이루어졌다.

이후 와일즈는 자신의 증명을 한 번 더 검증한 후 발표하려고 했는데, 마침 케임브리지에서 학회가 열린다는 소식을 듣고 모교이기도 한 그곳에서 증명을 발표하기로 했다. 증명이 너무 길어서 강연 기회를 더 달라고 스승님(존 코즈)에게 떼를 써서 3번의 강연기회를 얻어낸 후 차례대로 발표했는데, 어디서 새나갔는지 "와일즈가 페르마의 마지막 증명을 정말로 증명했다" 는 소문이 퍼져나갔고, 마지막 강연에서는 구름처럼 청중들이 몰려왔다고 한다. 발표 후에 사람들의 반응은 더 이상의 자세한 설명은 생략한다.

하지만 그의 증명에서 큰 문제가 발견된다.

3.6 첫 증명의 오류

케임브리지에서 와일즈가 증명을 발표한 후, 수학자들은 검증을 위해 와일즈의 논문에 달라붙었다. 이 작업에 참가한 사람 중에는 와일즈가 앞서 검증을 부탁했던 닉 카츠도 포함되어 있었는데…,

증명에서 오류가 발견되었다!

닉 카츠는 과거에 자신이 검증할 때는 못 찾았던 오류를 찾아내고 뒷목을 부여잡았지만 이미 때는 늦었다. 매의 눈으로 검증 작업을 지켜보던 수학자들 사이에 소문이 퍼지기 시작한 것이다. 이 과정에서 일어난 소동에 대해서는 더 이상의 자세한 설명은 생략한다. 전 세계의 수학자들이 열심히 설전을 벌이는 동안, 와일즈 본인은 다시금 은톨이 상태로 연구에 돌입했지만 성과를 얻지 못해 연구를 포기하려고도 했다. 이때 와일즈의 제자인 테일러가 콜리바긴-플라흐의 방법을 검토했는데 이것이 결정적인 힌트가 되었다.

1994년 9월 19일, 와일즈는 자신이 이용했던 이와자와 이론과 콜리바긴-플라흐의 방법이 서로를 보완하는 성질을 갖고 있다는 사실을 알아냈다. 두 가지 방법을 한데 합쳐놓으니 문제점이 해결됐다. 와일즈 왈,

"그것은 말로 표현할 수 없을 정도로 아름답고, 간결하면서 또 우아했어요. 왜 이 사실을 진작 발견하지 못했는지 이해가 가질 않았습니다. 정말 기쁘면서도 어이가 없어서 계산 결과를 한 20분 동안 멍하니 바라보았습니다. 그리고는 밖으로 나와 수학과 건물 내의 복도를 이리저리 거닐다가 다시 자리로 돌아와서는 제가 발견한 것이 아직 그대로 있는지 확인해 보았습니다. 꿈을 꾼 건지도 모르니까 말이죠. 그런데 그 아름다운 녀석이 여전히 그 자리에 있더군요. 저는 너무 흥분해서 정신을 가눌 수가 없었습니다. 제 연구 인생을 통틀어 가장 중요한 순간이었지요. 앞으로 제가 어떤 발견을 한다해도 그런 정도의 환희는 두 번 다시 느껴보지 못할 겁니다."

결국 와일즈는 첫 증명에서의 문제점을 해결하고 인류 역사에 길이 남을 낚시질에 마침표를 찍었다. 위에서 언급한 증명한 사람에게 10만 마르크를 지불한다는 상금도 수령했다. 다만 당시 10만 마르크가 여러 번의 디노미네이션을 거쳐 97년에 와일스가 수령한 것은 약 4만 달러 정도였다.

3.7 와일즈의 최종 증명

그 내용은 본 항목의 여백이 너무 좁아 여기에 적지는 않겠다. 그렇게 역사에 길이 남을 낚시질이 또다시.. 농담이 아니라 증명이 소설책 한 권 분량이라 여기에 옮기려면 항목을 몇 개 분할해도 부족할 정도다. 증명파일은 PDF파일 109쪽, ZIP으로 압축한 용량이 9.4메가라는 압도적인 포스를 자랑한다. 보고 싶은 사람은 다운로드보기

와일즈 교수는 이 증명 논문을 아내에게 생일 선물로 하였으며, 아내는 크게 기뻐했다. 국내에 번역된 사이먼 싱의 '페르마의 마지막 정리'에서는 "그렇게 기뻐하는 아내의 모습은 처음 봤다"고 되어 있는데, 와일즈가 증명을 완성하려고 얼마나 고생했는지를 옆에서 지켜본 아내이니 당연했을 것이다.

사실 와일즈가 석사과정에 입문할 때부터 매우 극적인 우연들이 겹쳐서 만들어낸 걸작이다. 예를 들자면, 왠지 모르게 베리 마주르가 여러 차례 활약을 했다.물론 세간은 그는 물론이거니와 리벳 조차 조명하지 않지만 리벳이 엡실론 추측을 증명할 때나, 와일즈가 모듈러가 아닌 소수의 타원곡선들 때문에 골머리를 앓고 있을 때 다른 프라임을 사용하게끔 영감을 준다거나. 물론 와일즈의 7년간의 집념과 능력이 가장 중요한 것이었음은 부정할 수 없을뿐더러 사실 학문이란 것은 이전의 다른 선구자들처럼 우연이나 운에서 깨달음을 얻으며 발전해왔다.

학구열에 불타 올라 이 증명을 구경해 보고 싶더라도 웬만하면 포기하는 게 정신 건강에 좋다. 대학교 수학과 석박사과정 정도는 되어야 읽는 게 가능한 수준이다. 행여나 목숨을 아끼질 않을 용감한 위키러들을 위해 논문의 서론 처음 두 줄을 소개하자면 이렇다.

Introduction.

An elliptic curve over Q is said to be modular if it has a finite covering by a modular curve of the for X₀(N). Any such elliptic curve has the property that its Hasse-Weil zeta function has an analytic continuation and satisfies a functional equation of the standard type.
(이하 생략)

글자도 못 읽겠지? 괜찮아 나도 그래
이 논문은 '타원곡선(elliptic curve)', '모듈러성 정리(modular)', '모듈러 곡선(modular curve)의 유한 덮개(finite covering)', '하세-베유 제타 함수(Hasse-Weil zeta function)의 해석적 연속(analytic continuation)', '표준형의 함수방정식(functional equation of the standard type)' 같은 표현이 당연히 무엇인지 알고 있다는 가정하에 쓰여 있다. 이게 대체 무슨 귀신 씨나락 까먹는 소리입니까 알고싶니? 그렇담 넌 수학과야! 거기에 수많은 기호와 수식은 덤이다. 이러한 난해한 내용이 100쪽 넘게 이어진다고 생각하면 된다. 그리고 서두에 밝힌 것은 지극히 기본적인 것들이고 이어서 수없이 많은 정리와 증명들, 예를 들어 L-함수, 갈루아 이론, 이와사와 이론, 유수 공식 등 물리학이나 통계학 전공자라 할지라도 평생토록 듣지 못할 괴이쩍은 것들이 쏟아져 나온다.

영국 UKTV에서 다큐멘터리도 제작되었다. 재생시간의 압박을 견딜 수 있다면 보시라

어쨌든 그렇게 해서, 페르마의 대정리는 드디어 증명되었다!

3.8 와일즈 외 새로운 증명

• 2012년 9월 19일. 일본 교토대학의 모치즈키 신이치(望月新一) 수리해석연구소 교수가 ABC추론을 증명했다고 밝혔는데 이것이 사실이라면 와일스가 증명해낸 방식보다는 비교적 간단하게 풀 수 있다고 한다. 그래도 여기에 올릴 수 있을 만큼 여백이 남아돌지는 않는 것 같다. 대충 저 100쪽짜리 증명이 반 정도로 줄어 든다고 한다. 오십보백보관련기사 하지만, 모치즈키가 ABC추론을 증명하기 위해 만든 이론인 Inter-Universal Teichmuller Theory는 561페이지에 다다르며 그 내용이 너무나 난해해서 현재 수학계에서 그의 이론을 제대로 이해한 사람이 거의 전무하며 실질적으로는 와일즈의 증명만큼 어려운 증명이다. 정말로 이해하는 사람이 없어서 이 증명이 공식적인 증명으로 받아들여지고 있지조차 않다.

• 포스텍 수학과 소속인 김민형 교수도 위상수학적인 접근방법을 정수론에 이용해서 페르마의 대정리를 증명하는 새로운 방법을 제시했고 이 업적으로 한국인 최초로 옥스포드 대학교 수학과 정교수로 임용됐다.

이밖에 페르마의 마지막 정리를 증명을 하기위해 근 삼백년간 학자들이 내놓은 증명들과, 와일즈를 필두로 한 최종 증명 과정은 페르마의 마지막 정리/증명 문서 참조.

4 와일즈의 수상이력

• 볼프스켈 상 : '페르마의 마지막 정리'를 해결한 사람에게 부여되는 상이다. 당연히 수상했다.

• 필즈상 특별상 : 1995년 5월 증명이 완성하자 와일즈는 수많은 상을 받았다. 하지만, 수학계의 노벨상이라고 할 만한 필즈상 수상에는 한 가지 문제가 있었다. 필즈상은 40세 이하의 젊은 수학자에게만 수여된다는 조건이 달려 있는데, 와일즈 교수가 완벽한 증명을 낼 때 그의 나이는 41세였다. 그렇다고, 상을 안 주기에는 그의 업적이 너무나 대단했기 때문에 국제 수학자 연맹에서 1998년에 특별상 형태로 기념 은판을 제작하여 수여했고, 필즈상 수상자 공식 명단에는 그 사실이 분명하게 기록되어 있다. 관련 pdf 문서

• 2000년에 와일즈는 대영 제국 훈장 2등급을 받았으며, 왕립 학회 회원도 되었다. 그래서 그의 현재의 이름은 Sir Andrew John Wiles, KBE, FRS이다. KBE는 위에서 설명한 대영 제국 훈장 2등급이고, FRS는 왕립 학회 회원(Fellow of Royal Society)이라는 뜻이다.

• 2016년 아벨상은 이 정리를 해결한 공로로 인해 수여되었다.

1993년에 와일즈가 처음으로 증명을 공개했을 때, 그는 뉴욕 타임스를 비롯한 세계 각지의 신문 1면을 장식했으며 1년 후 완벽한 증명을 완성했을 때도, 볼프스켈 상을 탔을 때도 그랬다. 페르마의 마지막 정리를 증명한 것이 얼마나 충격적이었는지 보여주는 사례다.

상은 아니지만 9999 Wiles라는 이름의 소행성은 그의 이름을 딴 것이다. 다른 과학자(천문학자)들이 그의 공로를 인정하여 헌정한 것이라고 보면 된다.

5 해결하지 못한 의문

경악과 찬사를 받으며 현대수학으로 간신히 증명된 이 정리는 해석학적으로 증명이 되었음을 생각해보면 당시의 수준으로는 증명이 불가능하다. 만일 페르마의 대정리가 성립하지 못함을 증명했다면 페르마의 '나는 이거 증명해냈음'이라는 말이 구라라고 결론내릴 수 있겠지만 이렇게 어려운 방법으로 증명이 되었다면 정말로 증명을 해냈는지 아닌지는 여전히 알 수 없으므로, 희대의 떡밥인 "여백이 부족하여 기록하지 않는다"는 여전히 미궁 속에 빠져 있다. 증명하는 데만 책 한 권 분량이라고 하니 귀찮을 법도 하다.

가장 일반적인 관점은 '오류를 발견하지 못 하고 증명했다고 착각했다'는 것. 실제로 n=4 인 경우에 대한 증명은 페르마 자신이 책에 적어놓았고, 이 아이디어를 이용하면 n=3 인 경우도 풀 수 있다. 다만, 이 일부의 경우를 증명한 것으로 모든 경우를 다 증명했다고 착각한 것일 수 있다. 어디까지나 취미로 수학을 했기에 아마추어였던 페르마는 증명에 그다지 공을 들이지 않는 편이었고, 암산으로 대충 맞으면 맞는다고 생각했다. 이래도 '천재'이기에 대부분이 맞아 떨어졌지만, 페르마의 대정리에서는 오류가 있었고, 굳이 종이를 사용해서 증명할 생각도 없었기에 오류를 모르고 넘어갔다는 것. 페르마는 자기가 정식으로 그 정리를 증명한 게 아니므로, 금방 자기 증명이 잘못된 것을 발견했더라도 굳이 책 여백에 써넣은 낙서를 수정할 필요는 느끼지 않았다는 추정도 있다.

결국 수백년 동안 수많은 학자들의 노력이 무용지물이었고 현대수학으로 겨우 증명되었기에 4백 년 전 인물인 페르마는 증명해내지 못 했을 것이라는 쪽이 학회의 전반적인 분위기다. 하지만 현대인들의 예측이 어긋날 수도, 어긋나지 않을 수도 있다. 증명을 했든 안 했든 페르마가 생각한 방법을 이제는 알 수 없겠지만 전혀 다른 획기적인 증명법으로 페르마의 대정리를 증명했었을지도 모른다. 이 때문에 페르마가 획기적인 다른 방법으로 실제로 문제를 해결했다고 믿는 사람도 있으며, 아직도 페르마가 증명했을 방법을 연구하는 사람도 있다. 솔직히 페르마 이 양반이 여간 천재여야지

현대수학 없이도 간단히 증명되는 '[math]n^x + n^y = n^z[/math] ([math]n \gt 2[/math]인 정수)일 때 정수해 ([math]x[/math], [math]y[/math], [math]z[/math])는 존재하지 않는다.'라는 명제와 혼동했을 거라는 얘기도 있다. 그럼 n=4일때의 증명을 적어놓은 게 말이 안 되잖아

6 우리의 문제를 돌려줘!

와일즈 교수는 증명을 끝낸 후 "새 문제 만들어주세요 현기증 난단 말이에요."라는 부탁에 시달렸다. 수학계의 오랜 난제인 페르마의 대정리가 증명되어 버리는 바람에, 이를 증명하려던 수많은 사람들이 목표를 잃고 좌절했기 때문이다.

그래서 나온 것이 7개의 밀레니엄 문제다. 문제의 선정에는 와일즈 교수를 포함한 여러 석학들이 참여했으며, 난제를 해결한 수학자들을 치하하기 위한 백만 달러라는 엄청난 상금까지 걸어 두었다. 더 많은 사람들이 수학에 관심을 가지도록 하기 위한 떡밥으로서 이런 상금을 부여한 것이다. 그런데 혹시라도, 증명에 성공한다면 백만 달러 따위는 문제가 아니다. 수학을 모르는 사람들에게도 이 문제를 푼 사람이라는 매스컴의 보도가 쏟아지고 수많은 사람들의 관심을 받게 될 것이니, 이 문제를 푼 사람에겐 부와 명예를 가져다주는 셈이다. 수학에 관심이 있다면 도전해보자.

7개의 문제중 1개는 증명이 완료되었다. 푸앵카레 추측이 해결되었는데, 이를 해결한 그 사람은 상금을 거절하면서 오히려 그 덕분에 더욱 더 유명해지게 되었다. 백만 달러를 거절한 사나이

7 어록

워낙 악명높은 정리여서 많은 이들이 이 정리에 대해 말을 남겼다.

페르마의 마지막 정리가 증명되기 전에 인류는 멸망할 것이다.

ㅡ 마지막 문제 그러나 멸망은 오지 않았습니다

그런 정리 따위에는 전혀 관심이 없다. 참인지 거짓인지 증명도 안 되는 명제 따위는 나도 얼마든지 만들 수 있다.

ㅡ 요한 카를 프리드리히 가우스(Johann Carl Friedrich Gauß)

이 문제는 황금알을 낳는 거위다.

ㅡ 다비트 힐베르트(David Hilbert)

제가 살아있는 동안은 증명되지 못 할 거라고 확신하고 있었습니다.

ㅡ 존 코츠(John Coates)

8 기타

• 뉴욕의 Eighth Street–New York University 지하철역에는 다음과 같은 낙서가 있다. 이것은 와일스 이전에 페르마의 정리를 증명했다고 주장한 미야오카의 기사가 나왔을 무렵에 쓰여진 것이라고 한다.

[math]x^n + y^n = z^n[/math] ([math]n \gt 2[/math]인 정수)일때 정수해 ([math]x[/math], [math]y[/math], [math]z[/math])는 존재하지 않는다, 나는 획기적인 방식으로 이 정리를 증명했다. 그러나 내가 탈 기차가 오고 있기 때문에 여기 적을 시간이 없다! 시간 부족의 정리

• 페르마의 소정리(Fermat's Little Theorem)는 소수에 관련된 내용으로, 페르마의 대정리와는 직접적인 연관은 없다. 해당항목 참조.

• 나무위키의 특징적 표현으로 자주 쓰이는 문구로, 너무 내용이 길어서 문서 링크를 할 때 사용한다.

17세기의 안알랴줌 이라고 한다.

• 여러 난제중에 가장 유명해서 그런지 중2병이 심한 사람들은 하나같이 학교를 졸업하면 이 문제를 풀겠다고 하는 경향이 있다. 이중 대부분은 풀린지 20년이 다 되어가는 이 문제가 아직 안 풀린 줄 알고 있는 게 대부분. 한 동안 블로그에 학교 졸업 후 계획에 페르마의 마지막 정리를 첫 번째로 밝히겠다는 이야기를 넣은 한 네덕의 짤이 유명해져 인터넷상에서 웃음거리가 된 적이 있었다.

9 대중 매체에서의 등장

• 각종 매체에서 수학정리 중 많이 언급되는 명제 중 하나다. 다른 명제는 '리만 가설', '골드바흐의 추측'이 있다.
• 수백 년 동안 증명이 안 되었었고, 가장 대중매체에 많이 언급된 탓이 큰 듯하다. 증명이 됐다고 발표한 날과 제대로 된 증명이 성공한 날 뉴욕 타임스 대문을 장식하기도 했다. 국내에서는 신문에 작게 기사가 난 것일 뿐이지만.
• 최종 증명 발표 이후에도 그는 계속 상을 받고 있으며, 대중매체에서는 '페르마의 마지막 정리를 증명한 사람'으로서 활약하고 있다. 스타 트렉에도 나왔을 정도.
• 일본의 수학 교양소설인 수학 걸 2권의 내용 중 하나가 주인공들이 정수론에 대해 공부하면서 n=4일 때 페르마의 마지막 정리의 보조정리(Lemma)를 증명하는 내용이다. 보조정리는 의외로 간단한데, '넓이가 제곱수인 직각삼각형은 존재하지 않는다.'이다. 수학 걸 2권의 부제가 페르마의 마지막 정리인 만큼, 원시 피타고라스 수가 무수히 많음을 증명하는 중고등학교 수준의 수학부터 시작해서 페르마의 마지막 정리의 증명에 결정적인 기여를 한 모듈러성 정리에 대한 설명에 이르기까지 상세하게 다루고 있으므로, 이에 대해 좀 더 알아보고 싶다면 한번 읽어보자. 주인공들이 중고등학생이라는 점이 함정(...) 국내 정식 발매명은 '수학 홀릭: 페르마의 마지막 정리'이다.
• 만화 금색의 갓슈벨에서는 응가 뿡뿡이 우마곤에게 문제로 냈다가 타카미네 키요마로에게 역관광당했다(…).
• 유희왕 ARC-V에서도 등장. 20화의 퀴즈 듀얼에서 라이프를 100, 300 같이 적게 걸고 나오는 수학 및 넌센스 퀴즈가 나오는데 뜬금포로 라이프 5,000을 걸고 나오는 "페르마의 대정리를 증명하시오"(...). 여기서 상대인 큐안도 에이타는 그런건 자기는 바로 푼다며 시청하던 이과생들을 격분하게 만들었다. 수학과 이과 관련 문제는 지지리도 모르는(...) 유우야는 당연히 모른다고 답했고, 그대로 유우야의 패배가 되는 줄 알았으나... 오히려 그 데미지를 에이타가 받게 한 후 역관광을 시전했다.
• 절대가련 칠드런에서 미나모토 코이치는 어렷던 시절부터 아주 똘똘하고 수재였던 터라 초등학교 5학년 동급생인 와카미야 나나코가 내는 수수께끼 퀴즈를 무심결에 전부 맞추고는 했다. 이에 화가난 와카미야는 아주 어려운 문제라고 하는 페르마의 대정리에 대해 물었고 미나모토는 또 그것을 덜컥 풀어버려(...) 난리가 났고, 아메리... 아니 코메리카로 유학가는 처지가 되었다.문제에만 집중하지 말고 출제자의 의도를 짐작하라고 ㅠㅠ
• 러키스타 15화에서 히이라기 카가미의 가족들이 모여서 퀴즈 프로그램을 보면서 문제를 푸는 장면이 나오는데, 페르마의 대정리를 다루는 나름대로 어려운 문제가 나오자 어려워서 가족들이 아무말도 안 하는 모습이 나온다. 카가미는 이걸 보면서 "왜 아는 문제는 누가 먼저랄것도 없이 잘 대답하면서 자신이 없으면 일제히 입을 다무는 걸까?"라고 묻는다.
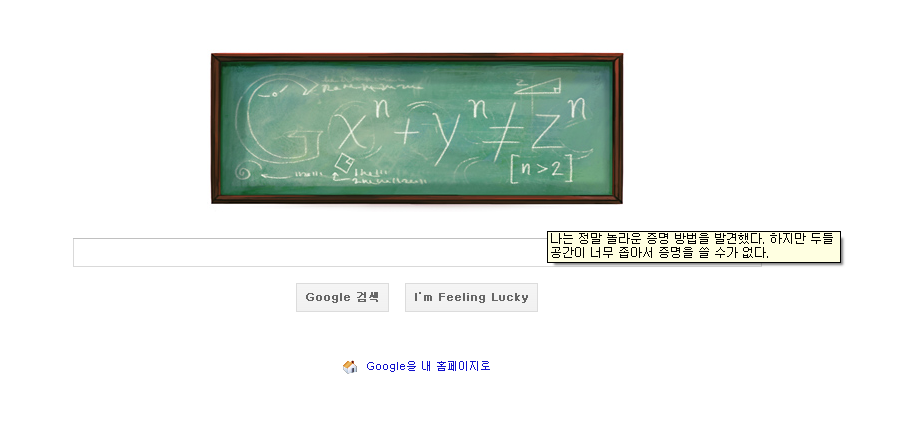
• 11대 닥터가 5시즌 1화에서 자신이 페르마에게 1줄을 알려주지 않고 잠들어버린 탓에 페르마가 증명을 완성하지 못했다고 언급한다. 그리고 그 다음날 알람을 잘못 맞춰서 페르마가 칼싸움하다 죽었다고 하는 건 덤
• 2011년, 페르마의 생일인 8월 17일에 페르마의 대정리가 구글 두들이 되었다.

• 다음 만화속세상 웹툰인 셜록: 여왕폐하의 탐정 53화에서는 셜록 홈즈가 이 문제를 이용해 악당을 엿먹이는 장면이 나온다. 해당 에피소드에서는 이것 이외에도 몬티 홀 문제 등 다양한 수학 개념들이 악당과 심리전을 펼치는 용도로 활용되었다.
• VOCALOID 카가미네 린·렌의 오리지널 곡인 우리들의 마지막 정리라는 곡은 여기서 모티브를 가져온 곡이다. 수학 공식이 가득한 곡이 아니라, 사회의 부조리한 강압에 대한 저항의식을 담은 곡. 이 세상이 잘못됐음을 당장은 고칠 수 없으나 후일 고쳐내겠다는 의지를 '우리의 마지막 정리도 틀리지 않았을 거라고, 지금 당장 증명할 수가 없을 뿐'이라는 가사로 담아냈다.